當前位置：試卷中心 > 試卷詳情

2021-2022學年廣西桂林市靈川中學高一（下）期中數學試卷

發布：2024/4/20 14:35:0

一、單項選擇題：本題共12小題，每小題4分，共48分，在每小題給出的四個選項中，有且只有一個選項是符合題目要求的。

1．與-80°角終邊相同的角是（　　）
A．80° B．280° C．240° D．100°
組卷：35引用：2難度：0.9
解析
2．函數y=4sinx+3在[-π，π]上的單調遞增區間為（　　）
A．[-π，
-
π
2
] B．[-
π
2
，
π
2
] C．[-π，
π
2
] D．[
π
2
，π]
組卷：93引用：3難度：0.8
解析
3．下列關于向量
a
，
b
的命題中，正確的是（　　）
A．若
|
a
|
=
|
b
|
，則
a
=
b
B．若
|
a
|
＞
|
b
|
，則
a
＞
b
C．若
a
=
b
，則
a
∥
b
D．若
a
∥
b
，則
a
與
b
夾角是0
組卷：9引用：1難度：0.7
解析
4．已知角α的終邊過點P（4，m）（m≠0），且
sinα
=
m
5
，則cosα的值為（　　）
A．±
3
5
B．
-
3
5
C．±
4
5
D．
4
5
組卷：601引用：5難度：0.7
解析
5．要得到函數
y
=
sin
（
2
x
+
π
3
）
的圖象，只須將函數y=sin2x的圖象（　　）
A．向左平移
π
3
B．向右平移
π
3
C．向左平移
π
6
D．向右平移
π
6
組卷：88引用：4難度：0.5
解析
6．已知
e
1
、
e
2
是平面內所有向量的一組基底，則下列四組向量中，不能作為基底的一組是（　　）
A．
e
1
+
e
2
和
e
1
-
2
e
2
B．
2
e
1
-
e
2
和
2
e
2
-
4
e
1
C．
e
1
-
2
e
2
和
e
1
D．
e
1
+
e
2
和
2
e
2
+
e
1
組卷：374引用：8難度：0.8
解析
7．已知
a
=
（
3
，
2
）
，
b
=
（
m
,-
1
）
，若
a
⊥
b
，則m=（　　）
A．
3
2
B．
-
3
2
C．
2
3
D．
-
2
3
組卷：67引用：6難度：0.7
解析
8．已知
a
=
sin
1
2
，
b
=
cos
π
6
，
c
=
tan
2
，則a、b、c的大小關系為（　　）
A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a
組卷：62引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題6小題，共70分，解答應寫出文字說明、證明過程及演算步驟。

25．已知函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖象，如圖所示．
（1）求函數f（x）的解析式；
（2）將函數f（x）的圖象向右平移
π
3
個單位長度，再將得到的圖象上各點的橫坐標縮短為原來的
1
2
，縱坐標不變，得到函數g（x）的圖象，當
x
∈
[
0
，
π
3
]
時，求函數g（x）的值域．
組卷：446引用：17難度：0.6
解析
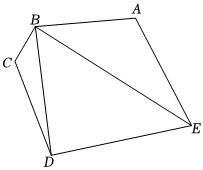26．為迎接2022年的亞運會，城市開始規劃公路自行車比賽的賽道，該賽道的平面示意圖為如圖所示的五邊形ABCDE．運動員在公路自行車比賽中如出現故障，可以在本隊的器材車、公共器材車或收容車上獲得幫助，也可以從固定修車點上獲得幫助．另外，為滿足需求，還需要運送一些補給物品，例如食物、飲料、工具和配件．所以項目設計需要預留出賽道內的兩條服務通BD，BE（不考慮寬度），已知E-D-C-B-A-E為賽道，∠BCD=∠BAE=
2
π
3
，∠CBD=
π
4
，CD=2
6
km,DE=8km.
（1）若∠CDE=
7
π
12
，求服務通道BE的長度；
（2）在（1）的條件下，應該如何設計，才能使折線賽道B-A-E最長（即BA+AE最大）？最長為多少？
組卷：13引用：2難度：0.5
解析