2022-2023學年重慶八中九年級（下）定時練習數學試卷（3.19）

一、選擇題：（本大題10個小題，每小題4分，共40分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側正確答案所對應的方框涂黑.

• 1．下列四個實數中，是正數的是（　　）

  A．-|-4|

  B． - 1 3

  C．-（-2）

  D．-12
  組卷：129引用：3難度：0.8

  解析

• 2．單項式

  -

  3

  5

  x

  的次數是（　　）

  A． - 3 5

  B．2

  C． 3 5

  D．1
  組卷：225引用：1難度：0.9

  解析

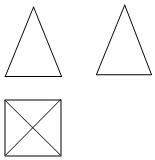• 3．如圖是某一幾何體的主視圖、左視圖、俯視圖，該幾何體是（　　）

  A．四棱柱

  B．四棱錐

  C．三棱柱

  D．三棱錐
  組卷：846引用：7難度：0.7

  解析

• 4．已知a＞b,則下列各式中一定成立的是（　　）

  A．a-b＜0

  B． a 3 ＞ b 3

  C．ac2＞bc2

  D．2a-1＜2b-1
  組卷：1305引用：22難度：0.8

  解析

• 5．若在反比例函數

  y

  =

  k

  x

  圖象的任一支上，y都隨x的增大而增大，則下列點可能在這個函數圖象上的為（　　）

  A．（-1，2）

  B．（3，2）

  C．（-2，-1）

  D．（0，-3）
  組卷：213引用：2難度：0.5

  解析

• 6．把黑色圓點按如圖所示的規律拼圖案，其中第①個圖案中有4個黑色圓點，第②個圖案中有6個黑色圓點，第③個圖案中有8個黑色圓點，…，按此規律排列下去，則第⑦個圖案中黑色圓點的個數為（　　）
  

  A．12

  B．14

  C．16

  D．18
  組卷：386引用：10難度：0.7

  解析

• 7．按如圖所示程序框圖計算，若輸入的值為x=16，則輸出結果為（　　）
  

  A． 2

  B．± 2

  C．4

  D．- 2
  組卷：797引用：13難度：0.8

  解析

• 8．如圖，AB是⊙O的直徑，點C、D是⊙O上的兩點，連接AC、OD、CD，且AC∥OD，若AB=6，∠ACD=15°，則AC的長為（　　）

  A． 2 2

  B．4

  C． 3 2

  D． 3 3
  組卷：269引用：2難度：0.6

  解析

三、解答題：（本大題共8個小題，19、20每小題8分，21-25題每小題8分，26題12分，共78分）解

• 25．如圖，拋物線y=ax²+bx+c與x軸交于A，B兩點，點B的坐標為

  （

  2

  ，

  0

  ）

  ，拋物線與y軸交于點C（0，-2

  2

  ），對稱軸為直線

  x

  =

  -

  3

  2

  2

  ，連接AC，過點B作BE∥AC交拋物線于點E．
  （1）求拋物線的解析式；
  （2）點P是線段AC下方拋物線上的一個動點，過點P作PF∥y軸交直線BE于點F，過點F作FD⊥AC交直線AC于點D，連接PD，求△FDP面積的最大值及此時點P的坐標；
  （3）在第（2）小問的條件下，將原拋物線沿著射線CB方向平移，平移后的拋物線過點B，點M在平移后拋物線的對稱軸上，點T是平面內任意一點，是否存在以B、P、M、T為頂點的四邊形是以BP為邊的菱形，若存在，直接寫出點T的坐標，若不存在，請說明理由．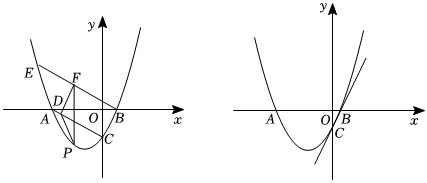
  
  組卷：383引用：2難度：0.2

  解析

• 26．在△ABC中，∠ACB=90°，點D是線段AC上一點，連接BD，過點C作CF⊥BD，垂足為點E，過點A作AF⊥CF于點F．
  （1）如圖1，如果設CF交AB于點G，且G為AB的中點，若

  AF

  =

  3

  ，∠ABC=60°，求線段AD的長；
  （2）如圖2，如果AC=BC，點E是線段CF的中點，過點E作EH⊥AC，垂足為點H，連接FH，求證：

  AH

  +

  HC

  2

  =

  2

  FH

  ；
  （3）如圖3，如果AC=BC=4，求FE的最大值．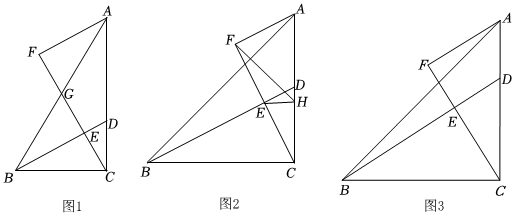
  
  組卷：690引用：3難度：0.3

  解析