2021-2022學年貴州省銅仁市沿河縣七年級（下）期中數學試卷

一、選擇題（本大題共10小題，每題4分，共40分）

• 1．下列各式由左到右的變形中，屬于因式分解的是（　　）

  A．（x+2）（x-1）=x2+x-2	B．x3+2x2+x=x（x2+2x+1）
  C．-a2-ab-ac=-a（a+b+c）	D．a2+b2=（a+b）2-2ab
  組卷：23引用：3難度：0.7

  解析

• 2．下列等式中，正確的是（　　）

  A．3a+2b=5ab	B．2（a-b）=2a-b
  C．（a+b）2=a2+b2	D．（-2a3）2=4a6
  組卷：14引用：2難度：0.7

  解析

• 3．計算

  （

  -

  7

  2

  ）

  2013

  ×

  （

  2

  7

  ）

  2012

  的結果是（　　）

  A．1

  B． - 7 2

  C． - 2 7

  D．-1
  組卷：35引用：2難度：0.8

  解析

• 4．將下列多項式因式分解，結果中不含有因式a+1的是（　　）

  A．a2-1	B．a2+a
  C．（a+2）2-2（a+2）+1	D．a2-a
  組卷：88引用：4難度：0.7

  解析

• 5．如果（x-2）（x+3）=x²+px+q,那么p、q的值為（　　）

  A．p=5，q=6

  B．p=1，q=-6

  C．p=1，q=6

  D．p=5，q=-6
  組卷：2790引用：38難度：0.9

  解析

• 6．《九章算術》是中國古代重要的數學著作，其中“盈不足術”記載：今有共買雞，人出九，盈十一；人出六，不足十六．問人數雞價各幾何？譯文：今有人合伙買雞，每人出九錢，會多出11錢；每人出6錢，又差16錢．問人數、買雞的錢數各是多少？設人數為x,買雞的錢數為y,可列方程組為（　　）

  A． 9 x + 11 = y 6 x + 16 = y	B． 9 x - 11 = y 6 x - 16 = y
  C． 9 x + 11 = y 6 x - 16 = y	D． 9 x - 11 = y 6 x + 16 = y
  組卷：2245引用：53難度：0.8

  解析

• 7．若（-x-y）（x²+y²）?A=x⁴-y⁴，則整式A為（　　）

  A．x+y

  B．x-y

  C．-x+y

  D．-x-y
  組卷：77引用：3難度：0.7

  解析

• 8．如圖，從邊長為（a+3）的正方形紙片中剪去一個邊長為3的正方形，剩余部分沿虛線又剪拼成一個如圖所示的長方形（不重疊，無縫隙），則拼成的長方形的另一邊長是（　　）
  

  A．a+3

  B．a+6

  C．2a+3

  D．2a+6
  組卷：1331引用：10難度：0.9

  解析

三、解答題（本大題共8個題，共86分）

• 23．已知：用2輛A型車和1輛B型車載滿貨物一次可運貨10噸；用1輛A型車和2輛B型車載滿貨物一次可運貨11噸．某物流公司現有31噸貨物，計劃同時租用A型車a輛，B型車b輛，一次運完，且恰好每輛車都載滿貨物．
  根據以上信息，解答下列問題：
  （1）1輛A型車和1輛B型車都載滿貨物一次可分別運貨多少噸？
  （2）請你幫該物流公司設計租車方案；
  （3）若A型車每輛需租金100元/次，B型車每輛需租金120元/次．請選出最省錢的租車方案，并求出最少租車費．
  組卷：5106引用：96難度：0.5

  解析

• 24．【閱讀與思考】
  整式乘法與因式分解是方向相反的變形．如何把二次三項式ax²+bx+c（a≠0）分解因式呢？
  我們已經知道：
  （a₁x+c₁）（a₂x+c₂）=a₁a₂x²+a₁c₂x+a₂c₁x+c₁c₂=a₁a₂x²+（a₁c₂+a₂c₁）x+c₁c₂．反過來，就得到：a₁a₂x²+（a₁c₂+a₂c₁）x+c₁c₂=（a₁x+c₁）（a₂x+c₂）．我們發現，二次三項式ax²+bx+c（a≠0）的二次項的系數a分解成a₁a₂，常數項c分解成c₁c₂，并且把a₁，a₂，c₁，c₂，如圖1所示擺放，按對角線交叉相乘再相加，就得到a₁c₂+a₂c₁，如果a₁c₂+a₂c₁的值正好等于ax²+bx+c的一次項系數b,那么ax²+bx+c就可以分解為（a₁x+c₁）（a₂x+c₂），其中a₁，c₁位于圖的上一行，a₂，c₂位于下一行，像這種借助畫十字交叉圖分解系數，從而幫助我們把二次三項式分解因式的方法，通常叫做“十字相乘法”．
  例如，將式子x²-x-6分解因式的具體步驟為：首先把二次項的系數1分解為兩個因數的積，即1=1×1，把常數項-6也分解為兩個因數的積，即-6=2×（-3）：然后把1，1，2，-3按圖2所示的擺放，按對角線交叉相乘再相加的方法，得到1×（-3）+1×2=-1，恰好等于一次項的系數-1，于是x²-x-6就可以分解為（x+2）（x-3）．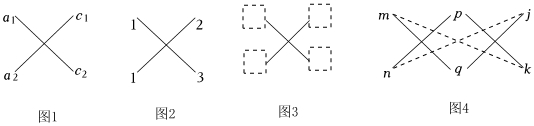
  
  請同學們認真觀察和思考，嘗試在圖3的虛線方框內填入適當的數，并用“十字相乘法”分解因式：x²+x-6=

  ．
  【理解與應用】
  請你仔細體會上述方法并嘗試對下面兩個二次三項式進行分解因式：
  （1）2x²+5x-7=

  ；
  （2）6x²-7xy+2y²=

  ；
  【探究與拓展】
  對于形如ax²+bxy+cy²+dx+ey+f的關于x,y的二元二次多項式也可以用“十字相乘法”來分解如圖4．將a分解成mn乘積作為一列，c分解成pq乘積作為第二列，f分解成jk乘積作為第三列，如果mq+np=b,pk+pj=e,mk+nj=d,即第1，2列、第2，3列和第1，3列都滿足十字相乘規則，則原式=（mx+py+j）（nx+qy+k），請你認真閱讀上述材料并嘗試挑戰下列問題．
  （1）分解因式3x²+5xy-2y²+x+9y-4=

  ；
  （2）若關于x,y的二元二次式x²+7xy-18y²-5x+my-24可以分解成兩個一次因式的積，求m的值．
  組卷：263引用：1難度：0.5

  解析