2022-2023學(xué)年陜西省西安市碑林區(qū)鐵一中學(xué)八年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．下列四個(gè)圖形中既是軸對(duì)稱圖形，又是中心對(duì)稱圖形的是（　　）

  A．等邊三角形

  B．角

  C．長方形

  D．平行四邊形
  組卷：70引用：2難度：0.8

  解析

• 2．下列等式從左到右的變形，屬于因式分解的是（　　）

  A．x2+2x-1=（x-1）2	B．（a+b）（a-b）=a2-b2
  C．x2+4x+4=（x+2）2	D．x2-4x+3=x（x-4）+3
  組卷：283引用：4難度：0.7

  解析

• 3．若m＞n,下列不等式不一定成立的是（　　）

  A．m+2＞n+2

  B．2m＞2n

  C． m 2 ＞ n 2

  D．m2＞n2
  組卷：7120引用：109難度：0.9

  解析

• 4．使式子

  1

  x

  -

  1

  有意義的x的取值范圍是（　　）

  A．x＞1

  B．x≠1

  C．x≥1

  D．x=1
  組卷：207引用：4難度：0.8

  解析

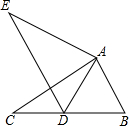• 5．如圖，在△ABC中，AB=2，BC=3.6，∠B=60°，將△ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)得到△ADE，當(dāng)點(diǎn)B的對(duì)應(yīng)點(diǎn)D恰好落在BC邊上時(shí)，則CD的長為（　　）

  A．1.6

  B．1.8

  C．2

  D．2.6
  組卷：3258引用：49難度：0.7

  解析

• 6．已知

  x = - 2

  y = 5

  是不等式kx+2y≤4的一個(gè)解，則整數(shù)k的最小值為（　　）

  A．3

  B．-3

  C．4

  D．-4
  組卷：448引用：4難度：0.7

  解析

• 7．在平面直角坐標(biāo)系中，已知線段AB的兩個(gè)端點(diǎn)坐標(biāo)分別為A（-1，-1），B（1，2），平移線段AB，平移后其中一個(gè)端點(diǎn)的坐標(biāo)為（3，-1），則另一端點(diǎn)的坐標(biāo)為（　　）

  A．（1，4）	B．（5，2）
  C．（-5，2）或（1，-4）	D．（1，-4）或（5，2）
  組卷：183引用：1難度：0.7

  解析

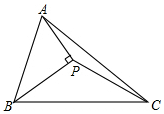• 8．如圖，BP是∠ABC的平分線，AP⊥BP于P，連接PC，若△ABC的面積為2cm²，則△PBC的面積為（　　）

  A．0.8cm2

  B．1cm2

  C．1.2cm2

  D．不能確定
  組卷：2860引用：10難度：0.4

  解析

三、解答題（共8題，共72分）

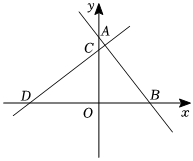• 23．如圖，在平面直角坐標(biāo)系中，直線

  y

  =

  -

  4

  3

  x

  +

  4

  分別與x軸、y軸交于點(diǎn)A、點(diǎn)B，將△AOB繞坐標(biāo)原點(diǎn)逆時(shí)針旋轉(zhuǎn)90°得到△COD．
  （1）求直線CD的函數(shù)表達(dá)式；
  （2）若點(diǎn)P是直線CD上一點(diǎn)，點(diǎn)Q是x軸上一點(diǎn)（點(diǎn)Q不與點(diǎn)O重合），當(dāng)△DPQ與△COD全等時(shí)，直接寫出點(diǎn)P的坐標(biāo)．
  組卷：590引用：2難度：0.1

  解析

• 24．（1）問題提出：
  如圖1，已知點(diǎn)C為線段BD上一動(dòng)點(diǎn)，分別過點(diǎn)B、D作AB⊥BD，ED⊥BD，連接AC、EC．已知AB=2，DE=1，BD=8，則AC+CE的最小值是

  ．
  （2）問題探究：
  如圖2，在四邊形ABCD中，AD∥BC，AD=BC，AB=6，BC=8，∠ABC=60°，E是四邊形ABCD內(nèi)一動(dòng)點(diǎn)，且

  S

  △

  EBC

  =

  1

  2

  S

  △

  EAD

  ，求EA+ED的最小值．
  （3）問題解決：
  如圖3，已知∠N=30°，長度為2的線段DE在射線NB上滑動(dòng)，點(diǎn)C在射線NA上，且NC=6，△CDE的兩個(gè)內(nèi)角的角平分線相交于點(diǎn)F，過F作FG⊥DE，垂足為G，求FG的最大值．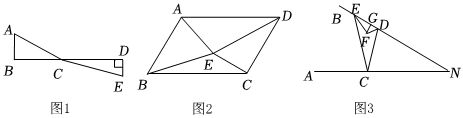
  
  組卷：384引用：2難度：0.1

  解析