2022-2023學年內蒙古包頭市鐵路一中高二（下）期末數學試卷（理科）

一、單選題（本大題共12小題，共60.0分）

• 1．已知U=R，A={x|x²-4x+3≤0}，B={x||x-3|＞1}，則A∪?_UB=（　　）

  A．{x|1≤x≤4}

  B．{x|2≤x≤3}

  C．{x|1≤x＜2}

  D．{x|2＜x≤3}
  組卷：641引用：11難度：0.8

  解析

• 2．復數

  5

  3

  +

  4

  i

  的共軛復數是（　　）

  A． 3 5 + 4 5 i

  B． 3 5 - 4 5 i

  C．3+4i

  D．3-4i
  組卷：149引用：65難度：0.9

  解析

• 3．函數f（x）=alnx+x在x=1處取到極值，則a的值為（　　）

  A． 1 2

  B．-1

  C．0

  D． - 1 2
  組卷：318引用：34難度：0.9

  解析

• 4．計算∫

  π

  2

  0

  cosxdx=（　　）

  A．-1

  B．1

  C． π 4

  D．0
  組卷：70引用：3難度：0.9

  解析

• 5．空間中，α，β，γ是三個互不重合的平面，l是一條直線，則下列命題中正確的是（　　）

  A．若α⊥β，l∥α，則l⊥β	B．若α⊥β，l⊥β，則l∥α
  C．若l⊥α，l∥β，則α⊥β	D．若l∥α，l∥β，則α∥β
  組卷：52引用：6難度：0.7

  解析

• 6．已知命題p：?x∈R，sinx＜1；命題q：?x∈R，e^|x|≥1，則下列命題中為真命題的是（　　）

  A．p∧q

  B．￢p∧q

  C．p∧￢q

  D．￢（p∨q）
  組卷：2551引用：61難度：0.8

  解析

• 7．命題“?x₀∈（0，+∞），lnx₀=x₀-1”的否定是（　　）

  A．?x0∈（0，+∞），lnx0≠x0-1	B．?x0?（0，+∞），lnx0=x0-1
  C．?x∈（0，+∞），lnx≠x-1	D．?x?（0，+∞），lnx=x-1
  組卷：4921引用：126難度：0.9

  解析

三、解答題（本大題共6小題，共70.0分）

• 21．已知函數f（x）=e^x-2x.
  （Ⅰ）求曲線y=f（x）在點（0，f（0））處的切線方程；
  （Ⅱ）若函數g（x）=f（x）-a,x∈[-1，1]恰有2個零點，求實數a的取值范圍．
  組卷：335引用：23難度：0.3

  解析

• 22．某商場為了考查商場一個月的商品銷售額y（單位：萬元）與廣告費支出x（單位：萬元）之間的相關關系，繪制了如圖散點圖．
  
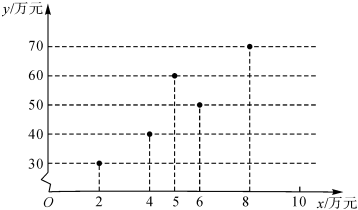
  （1）由散點圖求出y關于x的經驗回歸直線方程；
  （2）統計表明，該商場的某款廣告在平臺發布后，其商品日銷售額x（單位：萬元）近似地服從正態分布（5，1.69），商場對員工的獎勵方案如下：若日銷售額不超過2.4萬元，沒有獎勵；若日銷售額超過2.4萬元但不超過6.3萬元，則每人獎勵200元；若日銷售額超過6.3萬元，則每人獎勵500元，試求該商場每名員工單日獲得獎金的數學期望．（答案精確到整數）
  附：參考公式：經驗回歸直線方程=x+的斜率和截距的最小二乘估計分別為：

  ?

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  2

  i

  -

  n

  x

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ，
  若Z～N（μ，σ²），則P（μ-σ＜Z≤μ+σ）=0.6827，P（μ-2σ＜Z≤μ+2σ）=0.9545，P（μ-3σ＜Z≤μ+3σ）=0.9973．
  組卷：38引用：3難度：0.5

  解析