蘇教版（2019）必修第一冊 《第5章 函數概念與性質》2020年單元測試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．下列函數中，與函數

  y

  =

  -

  2

  x

  3

  相同的是（　　）

  A． y = x - 2 x

  B． y = - 2 x 3

  C． y = x 2 - 2 x

  D． y = - x - 2 x
  組卷：73引用：10難度：0.9

  解析

• 2．下列曲線能表示函數圖象的是（　　）

  A．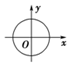

  B．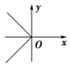

  C．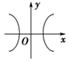

  D．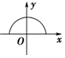
  組卷：152引用：1難度：0.7

  解析

• 3．已知f（x）=

  x + 1 ， x ＜ 0

  0 ， x = 0

  x - 1 ， x ＞ 0

  ，則f[f（

  2

  3

  ）]的值為（　　）

  A．- 1 3

  B． 1 3

  C． 2 3

  D．- 2 3
  組卷：28引用：3難度：0.9

  解析

• 4．已知函數y=f（x）是奇函數，當x＜0時，f（x）=x²+mx+1，且f（1）=-2，則實數m的值為（　　）

  A．-4

  B．0

  C．4

  D．2
  組卷：462引用：5難度：0.7

  解析

• 5．函數y=f（x）是R上的偶函數，且在（-∞，0]上是增函數，若f（a）≤f（2），則實數a的取值范圍是（　　）

  A．（-∞，2]	B．[-2，+∞）
  C．[-2，2]	D．（-∞，-2]∪[2，+∞）
  組卷：201引用：9難度：0.5

  解析

• 6．已知函數y=f（x）的定義域為（-∞，1）∪（1，+∞），且f（x+1）為奇函數，當x＜1時，f（x）=-x²-2x,則

  f

  （

  x

  ）

  =

  1

  2

  的所有根之和等于（　　）

  A．4

  B．5

  C．6

  D．12
  組卷：831引用：8難度：0.2

  解析

• 7．已知實數a≠0，函數f（x）=

  2 x + a , x ＜ 1

  - x - 2 a , x ≥ 1

  ，若f（1-a）=f（1+a），則a的值為（　　）

  A．- 3 2

  B．- 3 4

  C．- 3 4 或- 3 2

  D．-1
  組卷：508引用：8難度：0.7

  解析

四、解答題（本大題共6小題，共70分．解答時應寫出文字說明、證明過程或演算步驟）

• 21．已知二次函數y=f（x）滿足f（-2）=f（4）=-16，且f（x）最大值為2．
  （1）求函數y=f（x）的解析式；
  （2）求函數y=f（x）在[t,t+1]（t＞0）上的最大值．
  組卷：102引用：6難度：0.3

  解析

• 22．函數y=f（x）的定義域為R，若存在常數M＞0，使得|f（x）|≥M|x|對一切實數x均成立，則稱f（x）為“圓錐托底型”函數．
  （1）判斷函數f（x）=2x,g（x）=x³是否為“圓錐托底型”函數？并說明理由．
  （2）若f（x）=x²+1是“圓錐托底型”函數，求出M的最大值．
  組卷：444引用：3難度：0.5

  解析