2022-2023學(xué)年河南省開(kāi)封市五縣聯(lián)考高一（下）第二次月考數(shù)學(xué)試卷

一、單選題（本大題共8小題，共40分）

• 1．設(shè)（1+2i）（a+i）的實(shí)部與虛部相等，其中a為實(shí)數(shù)，則a等于（　　）

  A．-3

  B．-2

  C．2

  D．3
  組卷：5055引用：18難度：0.9

  解析

• 2．下列結(jié)論正確的是（　　）

  A．底面是正三角形的三棱錐是正三棱錐

  B．所有幾何體的表面都能展開(kāi)成平面圖形

  C．棱錐的側(cè)棱長(zhǎng)與底面多邊形的邊長(zhǎng)相等，則該棱錐可能是正六棱錐

  D．一個(gè)直角三角形繞其一條直角邊所在直線(xiàn)旋轉(zhuǎn)形成的封閉曲面所圍成的圖形叫做圓錐
  組卷：43引用：1難度：0.5

  解析

• 3．某學(xué)校共有980名學(xué)生，其中高一的學(xué)生有400名，高二的學(xué)生有300名，其余都是高三的學(xué)生，為了解該校學(xué)生的體育鍛煉時(shí)間，按照高一、高二、高三三個(gè)級(jí)段進(jìn)行分層抽樣，如果樣本容量為196，那么應(yīng)在高三的學(xué)生中抽取（　　）

  A．48名

  B．52名

  C．56名

  D．60名
  組卷：58引用：3難度：0.7

  解析

• 4．《九章算術(shù)》是我國(guó)數(shù)學(xué)史上堪與歐幾里得《幾何原本》相媲美的數(shù)學(xué)名著，其第五卷《商功》中有如下問(wèn)題：“今有圓堡，周四丈八尺，高一丈一尺，問(wèn)積幾何？“這里所說(shuō)的圓堡就是圓柱體，其底面周長(zhǎng)是4丈8尺，高1丈1尺，問(wèn)它的體積是多少？若π取3，估算該圓堡的體積為（　　）立方尺（1丈=10尺）．

  A．1998

  B．2012

  C．2112

  D．2324
  組卷：31引用：1難度：0.9

  解析

• 5．m,n為空間中兩條不重合直線(xiàn)，α為空間中一平面，則下列說(shuō)法正確的是（　　）

  A．若m∥n,n?α，則m∥α	B．若m⊥α，m∥n,則n⊥α
  C．若m∥α，n?α，則m∥n	D．若m⊥α，m⊥n,則n∥α
  組卷：67引用：7難度：0.7

  解析

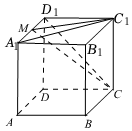• 6．如圖，在正方體ABCD-A₁B₁C₁D₁中，M為A₁D₁中點(diǎn)，過(guò)A₁C₁且與CD₁平行的平面交平面C₁CM于直線(xiàn)l,則直線(xiàn)l與AB所成角的余弦值是（　　）

  A． 3 2

  B． 2 2

  C． 6 + 2 4

  D． 6 3
  組卷：80引用：3難度：0.6

  解析

• 7．奔馳定理：已知O是△ABC內(nèi)的一點(diǎn)，△BOC，△AOC，△AOB的面積分別為S_A，S_B，S_C，則S_A?

  OA

  +S_B?

  OB

  +S_C?

  OC

  =

  0

  ．“奔馳定理”是平面向量中一個(gè)非常優(yōu)美的結(jié)論，因?yàn)檫@個(gè)定理對(duì)應(yīng)的圖形與“奔馳”轎車(chē)的logo很相似，故形象地稱(chēng)其為“奔馳定理”．設(shè)O為三角形ABC內(nèi)一點(diǎn)，且滿(mǎn)足

  OA

  +2

  OB

  +3

  OC

  =3

  AB

  +2

  BC

  +

  CA

  ，則

  S

  △

  AOB

  S

  △

  ABC

  =（　　）

  A． 2 5

  B． 1 2

  C． 1 6

  D． 1 3
  組卷：626引用：7難度：0.6

  解析

四、解答題（本大題共6小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明，證明過(guò)程或演算步驟）

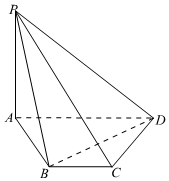• 21．如圖，在四棱錐P-ABCD中，AD=2，AB=BC=CD=1，BC∥AD，∠PAD=90°，∠PBA為銳角，平面PBA⊥平面PBD．
  （1）證明：PA⊥平面ABCD；
  （2）若AD與平面PBD所成角的正弦值為

  2

  4

  ，求二面角P-BD-C的余弦值．
  組卷：526引用：5難度：0.5

  解析

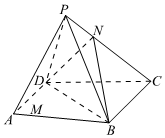• 22．如圖，在四棱錐P-ABCD中，底面ABCD為直角梯形，AD∥BC，∠ADC=90°，AD=CD=3，BC=4，△PBC為正三角形，點(diǎn)M，N分別在線(xiàn)段AD和PC上，且

  DM

  AM

  =

  CN

  PN

  =

  2

  ．設(shè)二面角P-AD-B為θ，且

  cosθ

  =

  1

  3

  ．
  （1）求證：PM∥平面BDN；
  （2）求直線(xiàn)PM與平面PBC所成角的正弦值；
  （3）求三棱錐P-ABN的體積．
  組卷：326引用：2難度：0.6

  解析