當前位置：試卷中心 > 試卷詳情

2022-2023學年河南省開封市通許縣等3地高二（下）期末數學試卷

發布：2024/5/23 8:0:8

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設集合A={x|log₂（x+2）＜2}，集合B={x|1≤2^x≤8}，則A∩B=（　　）
A．（0，2） B．（0，2] C．[0，2） D．[0，2]
組卷：103引用：3難度：0.8
解析
2．已知命題p：?x∈R，
sinx
+
cosx
≥
2
，則￢p為（　　）
A．?x∈R，
sinx
+
cosx
＜
2
B．?x?R，
sinx
+
cosx
＜
2
C．?x?R，
sinx
+
cosx
＜
2
D．?x∈R，
sinx
+
cosx
＜
2
組卷：34引用：3難度：0.8
解析
3．已知關于x的不等式x²-4ax+3a²＜0（a＜0）的解集為（x₁，x₂），則
x
1
+
x
2
+
a
x
1
x
2
的最大值是（　　）
A．
6
3
B．-
2
3
3
C．
4
3
3
D．
-
4
3
3
組卷：1247引用：35難度：0.9
解析
4．第19屆亞運會即將在西子湖畔——杭州召開，為了辦好這一屆“中國特色、浙江風采、杭州韻味、精彩紛呈”的體育文化盛會，杭州亞運會組委會決定進行賽會志愿者招募，在杭大學生紛紛踴躍參加．現有4名大學生志愿者，通過培訓后，擬安排在游泳、籃球、體操三個項目進行志愿者服務，假設每個項目至少安排一名志愿者，且每位志愿者只能參與其中一個項目，在甲被安排到游泳項目的條件下，乙也被安排到游泳項目的概率為（　　）
A．
1
12
B．
1
6
C．
1
4
D．
2
9
組卷：85引用：2難度：0.7
解析
5．設（3x-2）¹⁰⁰=a₀+a₁x+a₂x²+?+a₁₀₀x¹⁰⁰，若a₀+a₂+a₄+…+a₁₀₀+m=12k（k∈Z）．則實數m可能是（　　）
A．3 B．9 C．10 D．11
組卷：70引用：2難度：0.6
解析
6．為研究變量x,y的相關關系，收集得到下列五個樣本點（x,y）：

x 5 6.5 7 8 8.5

y 3 4 6 8 9

若由最小二乘法求得y關于x的回歸直線方程為
?
y
=
1
.
8
x
+
?
a
，則據此計算殘差為0的樣本點是（　　）
A．（6.5，4） B．（7，6） C．（8，8） D．（8.5，9）
組卷：10引用：3難度：0.6
解析
7．用四種顏色給正四棱錐V-ABCD的五個頂點涂色，要求每個頂點涂一種顏色，且每條棱的兩個頂點涂不同顏色，則不同的涂法有（　　）
A．72種 B．36種 C．12種 D．60種
組卷：459引用：9難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

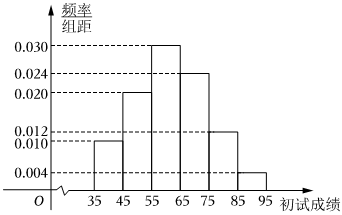21．某校數學組老師為了解學生數學學科核心素養整體發展水平，組織本校8000名學生進行針對性檢測（檢測分為初試和復試），并隨機抽取了100名學生的初試成績，繪制了頻率分布直方圖，如圖所示．
（1）根據頻率分布直方圖，求樣本平均數的估計值；
（2）若所有學生的初試成績X近似服從正態分布N（μ，σ²），其中μ為樣本平均數的估計值，σ≈14．初試成績不低于90分的學生才能參加復試，試估計能參加復試的人數；
（3）復試共三道題，規定：全部答對獲得一等獎；答對兩道題獲得二等獎；答對一道題獲得三等獎；全部答錯不獲獎．已知某學生進入了復試，他在復試中前兩道題答對的概率均為a,第三道題答對的概率為b.若他獲得一等獎的概率為
1
8
，設他獲得二等獎的概率為P，求P的最小值．
附：若隨機變量X服從正態分布N（μ，σ²），則P（μ-σ＜X≤μ+σ）≈0.6827，P（μ-2σ＜X≤μ+2σ）≈0.9545，P（μ-3σ＜X≤μ+3σ）≈0.9973．
組卷：695引用：12難度：0.6
解析
22．已知函數f（x）=（a+1）e^x+
a
e
x
-3，其中e為自然對數的底數，a∈R．
（1）討論函數f（x）的單調性；
（2）當a=0時，若存在x∈R使得關于x的不等式k≥xf（x）成立，求k的最小整數值．（參考數據：
e
3
4
≈2.1）
組卷：27引用：1難度：0.2
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．?x∈R， sinx + cosx ＜ 2	B．?x?R， sinx + cosx ＜ 2
C．?x?R， sinx + cosx ＜ 2	D．?x∈R， sinx + cosx ＜ 2

x	5	6.5	7	8	8.5
y	3	4	6	8	9

2022-2023學年河南省開封市通許縣等3地高二（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設集合A={x|log2（x+2）＜2}，集合B={x|1≤2x≤8}，則A∩B=（ ）

2．已知命題p：?x∈R，sinx+cosx≥2，則￢p為（ ）

3．已知關于x的不等式x2-4ax+3a2＜0（a＜0）的解集為（x1，x2），則x1+x2+ax1x2的最大值是（ ）

5．設（3x-2）100=a0+a1x+a2x2+?+a100x100，若a0+a2+a4+…+a100+m=12k（k∈Z）．則實數m可能是（ ）

6．為研究變量x,y的相關關系，收集得到下列五個樣本點（x,y）： x 5 6.5 7 8 8.5 y 3 4 6 8 9 若由最小二乘法求得y關于x的回歸直線方程為?y=1.8x+?a，則據此計算殘差為0的樣本點是（ ）

7．用四種顏色給正四棱錐V-ABCD的五個頂點涂色，要求每個頂點涂一種顏色，且每條棱的兩個頂點涂不同顏色，則不同的涂法有（ ）

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

22．已知函數f（x）=（a+1）ex+aex-3，其中e為自然對數的底數，a∈R．（1）討論函數f（x）的單調性；（2）當a=0時，若存在x∈R使得關于x的不等式k≥xf（x）成立，求k的最小整數值．（參考數據：e34≈2.1）

1．設集合A={x|log₂（x+2）＜2}，集合B={x|1≤2^x≤8}，則A∩B=（　　）

2．已知命題p：?x∈R，
sinx
+
cosx
≥
2
，則￢p為（　　）

3．已知關于x的不等式x²-4ax+3a²＜0（a＜0）的解集為（x₁，x₂），則
x
1
+
x
2
+
a
x
1
x
2
的最大值是（　　）

5．設（3x-2）¹⁰⁰=a₀+a₁x+a₂x²+?+a₁₀₀x¹⁰⁰，若a₀+a₂+a₄+…+a₁₀₀+m=12k（k∈Z）．則實數m可能是（　　）

6．為研究變量x,y的相關關系，收集得到下列五個樣本點（x,y）：

x 5 6.5 7 8 8.5

y 3 4 6 8 9

若由最小二乘法求得y關于x的回歸直線方程為
?
y
=
1
.
8
x
+
?
a
，則據此計算殘差為0的樣本點是（　　）

7．用四種顏色給正四棱錐V-ABCD的五個頂點涂色，要求每個頂點涂一種顏色，且每條棱的兩個頂點涂不同顏色，則不同的涂法有（　　）

22．已知函數f（x）=（a+1）e^x+
a
e
x
-3，其中e為自然對數的底數，a∈R．
（1）討論函數f（x）的單調性；
（2）當a=0時，若存在x∈R使得關于x的不等式k≥xf（x）成立，求k的最小整數值．（參考數據：
e
3
4
≈2.1）