2022-2023學年上海市寶山區高一（下）期末數學試卷

一.填空題（第1-6題每題4分，第7-12題每題5分，滿分53分）

• 1．在復數范圍內，-4的所有平方根為

  ．
  組卷：55引用：1難度：0.8

  解析

• 2．若冪函數f（x）=（m²-5m+1）x^m+1為奇函數，則該函數的表達式f（x）=

  ．
  組卷：119引用：1難度：0.7

  解析

• 3．無論a為何值，函數y=a^x-3+1（a＞0，a≠1）的圖像恒經過一個定點，該定點坐標為

  ．
  組卷：137引用：2難度：0.7

  解析

• 4．若log₃2=m,則log₂96=

  （用含m的式子表示）．
  組卷：133引用：1難度：0.7

  解析

• 5．若向量

  a

  、

  b

  滿足

  ?

  a

  ，

  b

  ?

  =

  60

  °

  ，

  |

  a

  |

  =

  |

  b

  |

  =

  3

  ，則

  |

  a

  -

  2

  b

  |

  =

  ．
  組卷：43引用：1難度：0.7

  解析

• 6．已知集合

  A

  =

  {

  x

  |

  1

  +

  x

  1

  -

  x

  ＞

  0

  }

  ，集合B={x||x-a|＜2}，若A?B，則實數a的取值范圍是

  ．
  組卷：245引用：1難度：0.8

  解析

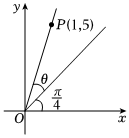• 7．在平面直角坐標系xOy中，銳角θ的大小如圖所示，則tanθ=

  ．
  組卷：57引用：1難度：0.8

  解析

三.解答題（本大題共有5題，滿分0分）

• 20．已知向量

  m

  =

  （

  sinx

  ,

  3

  cosx

  ）

  ，

  n

  =

  （

  sinx

  +

  2

  3

  cosx

  ,

  cosx

  ）

  ，令函數

  f

  （

  x

  ）

  =

  m

  ?

  n

  ．
  （1）求函數y=f（x）的表達式及其單調增區間；
  （2）將函數y=f（x）的圖像向右平移t（t＞0）個單位得到函數y=g（x）的圖像，且滿足g（-x）=g（x），當t最小時，存在實數x₁、x₂使得f（x₁）-g（x₂）=4，求|x₁-x₂|的最小值．
  組卷：65引用：2難度：0.5

  解析

• 21．在數學中，雙曲函數是與三角函數類似的函數，最基本的雙曲函數是雙曲正弦函數與雙曲余弦函數，其中雙曲正弦函數：

  sinh

  （

  x

  ）

  =

  e

  x

  -

  e

  -

  x

  2

  ，雙曲余弦函數：

  cosh

  （

  x

  ）

  =

  e

  x

  +

  e

  -

  x

  2

  ．（e是自然對數的底數，e=2.71828?）．
  （1）計算cosh（2）-2cosh²（1）的值；
  （2）類比兩角和的余弦公式，寫出兩角和的雙曲余弦公式：cosh（x+y）=_____，并加以證明；
  （3）若對任意t∈[0，ln2]，關于x的方程sinh（t）+cosh（x）=a有解，求實數a的取值范圍．
  組卷：61引用：4難度：0.5

  解析