2010-2011學年四川省成都七中高二（上）數學單元測試：立體幾何（2）

一．選擇題（每小題5分，共60分）

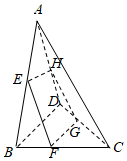• 1．如圖，在空間四邊形ABCD中，點E、H分別是邊AB、AD的中點，F、G分別是邊BC、CD上的點，且

  CF

  CB

  =

  CG

  CD

  =

  2

  3

  ，則（　　）

  A．EF與GH互相平行

  B．EF與GH異面

  C．EF與GH的交點M可能在直線AC上，也可能不在直線AC上

  D．EF與GH的交點M一定在直線AC上
  組卷：1157引用：26難度：0.9

  解析

• 2．下列說法正確的是（　　）

  A．直線a平行于平面M，則a平行于M內的任意一條直線

  B．直線a與平面M相交，則a不平行于M內的任意一條直線

  C．直線a不垂直于平面M，則a不垂直于M內的任意一條直線

  D．直線a不垂直于平面M，則過a的平面不垂直于M
  組卷：211引用：5難度：0.9

  解析

• 3．三棱錐P-ABC中，M為BC的中點，以

  PA

  ，

  PB

  ，

  PC

  為基底，則

  AM

  可表示為（　　）

  A． AM = PA - PB - PC	B． AM = PB + PC - PA
  C． AM = PA - 12 PB - 12 PC	D． AM = 12 PB + 12 PC - PA
  組卷：81引用：1難度：0.9

  解析

• 4．向量

  a

  ，

  b

  滿足：

  |

  a

  |

  =

  |

  b

  |

  =

  4

  ，

  ＜

  a

  ，

  b

  ＞

  =

  π

  3

  ，則|

  a

  -

  b

  |=（　　）

  A．4

  B．8

  C．37

  D．13
  組卷：127引用：1難度：0.9

  解析

• 5．平面α外一點P到平面α內的四邊形的四條邊的距離都相等，且P在α內的射影在四邊形內部，則四邊形是（　　）

  A．梯形	B．圓外切四邊形
  C．圓內接四邊形	D．任意四邊形
  組卷：38引用：2難度：0.9

  解析

• 6．已知m、n是不重合的直線，α、β是不重合的平面，有下列命題：
  ①若m?α，n∥α，則m∥n；
  ②若m∥α，m∥β，則α∥β；
  ③若α∩β=n,m∥n,則m∥α且m∥β；
  ④若m⊥α，m⊥β，則α∥β．
  其中真命題的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：1705引用：30難度：0.5

  解析

三．解答題（共66分）

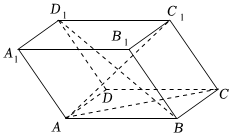• 19．已知平行六面體ABCD-A₁B₁C₁D₁中，底面ABCD是邊長為a的正方形，側棱AA₁的長為b,∠A₁AB=∠A₁AD=120°．
  （Ⅰ）求對角線AC₁的長．
  （Ⅱ）求直線BD₁和AC的夾角．
  組卷：135引用：1難度：0.5

  解析

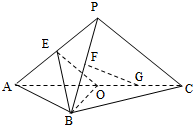• 20．如圖，平面PAC⊥平面ABC，△ABC是以AC為斜邊的等腰直角三角形，E，F，O分別為PA，PB，AC的中點，AC=16，PA=PC=10．
  （Ⅰ）設G是OC的中點，證明：FG∥平面BOE；
  （Ⅱ）證明：在△ABO內存在一點M，使FM⊥平面BOE，并求點M到OA，OB的距離．
  組卷：1127引用：15難度：0.1

  解析