當前位置：試卷中心 > 試卷詳情

2022-2023學年西藏拉薩第二高級中學高一（上）期末數學試卷

發布：2024/4/20 14:35:0

1．若集合M={-1，1}，N={-2，1，0}，則M∩N=（　　）
A．{0．-1} B．{0} C．{1} D．{-1，1}
組卷：2225引用：44難度：0.9
解析
2．命題“?x∈R，x²+x+1＞0“的否定為（　　）
A．?x∈R，x²+x+1≤0 B．??R，x²+x+1≤0
C．
?
x
0
∈
R
，
x
0
2
+
x
0
+
1
≤
0
D．
?
x
0
?
R
，
x
0
2
+
x
0
+
1
≤
0
組卷：90引用：8難度：0.8
解析
3．函數
f
（
x
）
=
2
x
-
3
的定義域為（　　）
A．
[
3
2
，
+
∞
）
B．
（
-
∞
，
3
4
]
C．（-∞，3）∪（3，+∞） D．（3，+∞）
組卷：136引用：2難度：0.7
解析
4．若
1
a
＜
1
b
＜
0
，則下列不等式中不正確的是（　　）
A．a+b＜ab B．
b
a
+
a
b
＞
2
C．ab＞b² D．a²＜b²
組卷：110引用：4難度：0.7
解析
5．不等式3x²-x-2≥0的解集是（　　）
A．
{
x
|
-
2
3
≤
x
≤
1
}
B．
{
x
|
-
1
≤
x
≤
2
3
}
C．
{
x
|
x
≤
-
2
3
或
x
≥
1
}
D．
{
x
|
x
≤
-
1
或
x
≥
2
3
}
組卷：1697引用：15難度：0.8
解析
6．已知冪函數f（x）=k?x^α（k∈R，α∈R）的圖象經過點
（
4
，
1
2
）
，則k+α=（　　）
A．
1
2
B．1 C．
3
2
D．2
組卷：597引用：9難度：0.8
解析
7．函數f（x）的圖象如圖所示，則（　　）
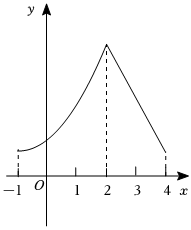
A．函數f（x）在[-1，2]上單調遞增
B．函數f（x）在[-1，2]上單調遞減
C．函數f（x）在[-1，4]上單調遞減
D．函數f（x）在[2，4]上單調遞增
組卷：20引用：1難度：0.7
解析

21．已知函數f（x）=log_a（1-x）+log_a（x+3）（0＜a＜1）．
（Ⅰ）求函數f（x）的定義域；
（Ⅱ）若函數f（x）的最小值為-4，求實數a的值．
組卷：282引用：38難度：0.3
解析
22．已知函數
f
（
x
）
=
ax
-
b
x
，其中a、b為非零實數，
f
（
1
2
）
=
-
1
2
，
f
（
2
）
=
7
4

（1）判斷函數的奇偶性，并求a、b的值；
（2）用定義證明f（x）在（0，+∞）上是增函數．
組卷：207引用：6難度：0.5
解析

A．?x∈R，x²+x+1≤0	B．??R，x²+x+1≤0
C． ? x 0 ∈ R ， x 0 2 + x 0 + 1 ≤ 0	D． ? x 0 ? R ， x 0 2 + x 0 + 1 ≤ 0

A． [ 3 2 ， + ∞ ）	B．（ - ∞ ， 3 4 ]
C．（-∞，3）∪（3，+∞）	D．（3，+∞）

A． { x \| - 2 3 ≤ x ≤ 1 }	B． { x \| - 1 ≤ x ≤ 2 3 }
C． { x \| x ≤ - 2 3 或 x ≥ 1 }	D． { x \| x ≤ - 1 或 x ≥ 2 3 }

1．若集合M={-1，1}，N={-2，1，0}，則M∩N=（ ）