2020-2021學年四川師大一中麓山校區八年級（下）期中數學試卷

一、選擇題（共十題：共30分）

• 1．在下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：142引用：6難度：0.8

  解析

• 2．如果a＞b,那么下列各項中正確的是（　　）

  A．a-2＜b-2

  B．-3a＜-3b

  C． a 2 ＜ b 2

  D．-a＞-b
  組卷：149引用：6難度：0.8

  解析

• 3．等腰三角形的一個角為50°，則它的底角為（　　）

  A．50°

  B．65°

  C．50°或65°

  D．80°
  組卷：1237引用：69難度：0.9

  解析

• 4．下列分解因式中，正確的是（　　）

  A．3m2-6m=3m（m-3）	B．a2b+ab+a=a（ab+b）
  C．x2+y2=（x+y）2	D．-x2+2xy-y2=-（x-y）2
  組卷：483引用：5難度：0.9

  解析

• 5．下列計算正確的是（　　）

  A．1+ 1 a = 2 a	B． 1 a - b - 1 b - a = 0
  C．a÷b? 1 b =a	D． - a - b a + b = - 1
  組卷：1027引用：10難度：0.8

  解析

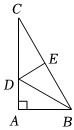• 6．如圖，在Rt△ABC中，∠A=90°，∠C=30°，BC的垂直平分線交AC于點D，并交BC于點E．若ED=2，則AC的長為（　　）

  A． 2 3

  B．4

  C．6

  D．8
  組卷：32引用：1難度：0.7

  解析

• 7．如圖，在平面直角坐標系中，等腰直角三角形ABC的頂點B與原點O重合，頂點A、C分別在y軸、x軸的正半軸上，將Rt△ABC沿直線y=2x向上平移得到Rt△A′B′C′，點B′的縱坐標為4，若AB=BC=3，則點A′的坐標為（　　）

  A．（3，7）

  B．（2，7）

  C．（3，5）

  D．（2，5）
  組卷：536引用：9難度：0.7

  解析

四、解答題（共三題：共30分）

• 21．【問題探究】
  如圖1，銳角△ABC中，分別以AB、AC為邊向外作等腰直角△ABE和等腰直角△ACD，使AE=AB，AD=AC，∠BAE=∠CAD=90°，連接BD，CE，試猜想BD與CE的大小關系，不需要證明．
  【深入探究】
  （1）如圖2，銳角△ABC中分別以AB、AC為邊向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，連接BD、CE，試猜想BD與CE的大小關系，并說明理由；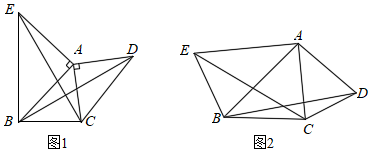
  
  【拓展應用】
  （2）如圖3，在△ABC中，∠ACB=45°，以AB為直角邊，A為直角頂點向外作等腰直角△ABD，連接CD，若AC=

  2

  ，BC=3，則CD長為

  ；
  （3）如圖4，已知在平面直角坐標系xOy中，O為坐標原點，A（0，3

  3

  ）、P（3，0），過點P作直線l⊥x軸，點B是直線l上的一個動點，線段AB繞點A按逆時針方向旋轉30°得到線段AC，則AC+PC的最小值為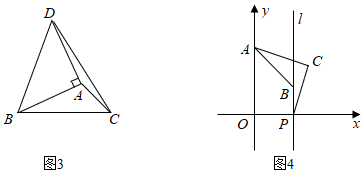

  ．
  
  組卷：891引用：2難度：0.1

  解析

• 22．已知直線l₁：y=-x+b與x軸交于點A，直線l₂：y=

  4

  3

  x-

  16

  3

  與x軸交于點B，直線l₁、l₂交于點C，且C點的橫坐標為1．
  （1）如圖1，過點A作x軸的垂線，若點P（x,2）為垂線上的一個點，Q是y軸上一動點，若S_△CPQ=5，求此時點Q的坐標；
  （2）若P在過A作x軸的垂線上，點Q為y軸上的一個動點，當CP+PQ+QA的值最小時，求此時P的坐標；
  （3）如圖2，點E的坐標為（-2，0），將直線l₁繞點C旋轉，使旋轉后的直線l₃剛好過點E，過點C作平行于x軸的直線l₄，點M、N分別為直線l₃、l₄上的兩個動點，是否存在點M、N，使得△BMN是以M點為直角頂點的等腰直角三角形？若存在，求出N點的坐標；若不存在，請說明理由．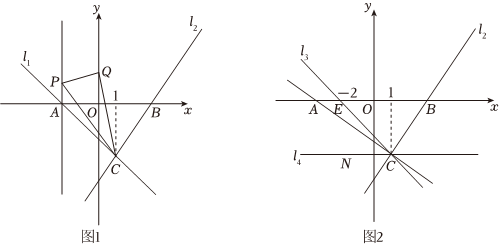
  
  組卷：1570引用：4難度：0.3

  解析