2023年山東省濟南市市中區育英中學中考數學三模試卷

一、選擇題（共10小題）

• 1．-

  1

  7

  的絕對值是（　　）

  A．-7

  B．7

  C．- 1 7

  D． 1 7
  組卷：1879引用：9難度：0.9

  解析

• 2．如圖是由幾個小正方體組成的幾何體，它的左視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：360引用：9難度：0.8

  解析

• 3．2021年3月5日，李克強總理在政府工作報告中指出，我國脫貧攻堅成果舉世矚目，5575萬農村貧困人口實現脫貧．5575萬=55750000，用科學記數法將55750000表示為（　　）

  A．5575×104

  B．55.75×105

  C．5.575×107

  D．0.5575×108
  組卷：947引用：9難度：0.8

  解析

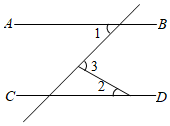• 4．如圖，AB∥CD，∠1=45°，∠2=35°，則∠3的度數為（　　）

  A．55°

  B．75°

  C．80°

  D．105°
  組卷：895引用：18難度：0.7

  解析

• 5．下列運算正確的是（　　）

  A．2a-a=2	B．（a-1）2=a2-1
  C．（2a3）2=4a6	D．a6÷a3=a2
  組卷：632引用：25難度：0.7

  解析

• 6．下列圖形中既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：30引用：1難度：0.8

  解析

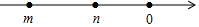• 7．實數m,n在數軸上的對應點如圖所示，則下列各式子正確的是（　　）

  A．m＞n

  B．-n＞|m|

  C．-m＞|n|

  D．|m|＜|n|
  組卷：5358引用：35難度：0.7

  解析

• 8．如圖顯示了用計算機模擬隨機拋擲一枚硬幣的某次實驗的結果
  
  下面有三個推斷：
  ①當拋擲次數是100時，計算機記錄“正面向上”的次數是47，所以“正面向上”的概率是0.47；
  ②隨著試驗次數的增加，“正面向上”的頻率總在0.5附近擺動，顯示出一定的穩定性，可以估計“正面向上”的概率是0.5；
  ③若再次用計算機模擬此實驗，則當拋擲次數為150時，“正面向上”的頻率一定是0.45．
  其中合理的是（　　）

  A．①

  B．②

  C．①②

  D．①③
  組卷：2001引用：22難度：0.7

  解析

三、解答題

• 24．平面內，先將一個多邊形以自身的一個頂點為位似中心放大或縮小，再將所得多邊形沿過該點的直線翻折，稱這種變換為自位似軸對稱變換，變換前后的圖形成自位似軸對稱．例如：如圖1，先將△ABC以點A為位似中心縮小，得到△ADE，再將△ADE沿過點A的直線l翻折，得到△AFG，則△ABC和△AFG成自位似軸對稱．
  
  （1）如圖2，在△ABC中，∠ACB=90°，AC＜BC，CD⊥AB，垂足為D．下列3對三角形：①△ABC和△ACD；②△BAC和△BCD；③△DAC和△DCB．其中成自位似軸對稱的是

  ；（填寫所有符合要求的序號）
  （2）在（1）答案最大序號圖形中，AC=3，BC=4，設自位似軸對稱變換的對稱軸與CD交于點E，求CE；
  （3）如圖4，在△ABC中，D是BC的中點，E為△ABC內一點，∠ABE=∠C，∠BAE=∠CAD，連接DE，求證：DE∥AC．
  組卷：222引用：1難度：0.1

  解析

• 25．如圖（1），二次函數y=x²+bx+c的圖象與x軸交于A，B兩點，與y軸交于C點，點B的坐標為（3，0），點C的坐標為（0，-3），直線l經過B，C兩點．
  （1）求二次函數的表達式；
  （2）點P為直線l上的一點，過點P作x軸的垂線與該二次函數的圖象相交于點M，再過點M作y軸的垂線與該二次函數的圖象相交于另一點N，當PM=MN時，求點P的橫坐標；
  （3）如圖（2），點C關于x軸的對稱點為點D，點P為線段上BC的一個動點，連接AP；點Q為線段AP上一點，且AQ=3PQ，連接DQ，求3AP+4DQ的最小值

  （直接寫出答案）．
  
  組卷：986引用：3難度：0.1

  解析