2022-2023學(xué)年河南省駐馬店市高一（下）期末數(shù)學(xué)試卷

一、單選題：本大題共8小題，每小題5分，共40分.在每個小題給出的四個選項中，只有一項是符合題目要求的.

• 1．如果點A在直線a上，而直線a又在平面α內(nèi)，那么可以記作（　　）

  A．A?a,a?α

  B．A∈a,a?α

  C．A?a,a∈α

  D．A∈a,a∈α
  組卷：44引用：4難度：0.9

  解析

• 2．與sin2023°的值最接近的數(shù)是（　　）

  A． 1 2

  B． 2 2

  C． - 1 2

  D． - 2 2
  組卷：77引用：2難度：0.8

  解析

• 3．已知矩形ABCD的對角線相交于點O，則

  AO

  -

  BC

  =（　　）

  A． AB

  B． AC

  C． OC

  D． OB
  組卷：272引用：2難度：0.8

  解析

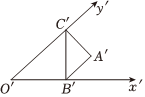• 4．用斜二測畫法畫△ABC的直觀圖如圖所示，其中O′B′=B′C′=2，

  A

  ′

  B

  ′

  =

  A

  ′

  C

  ′

  =

  2

  ，則△ABC中BC邊上的中線長為（　　）

  A． 3

  B． 2 3

  C．3

  D．1
  組卷：119引用：2難度：0.7

  解析

• 5．在復(fù)平面內(nèi)，角α的頂點為坐標原點，始邊為實軸非負半軸，終邊經(jīng)過復(fù)數(shù)

  Z

  =

  1

  -

  3

  i

  所對應(yīng)的點，則cosα=（　　）

  A． - 1 2

  B． 1 2

  C． 2 2

  D． 3 2
  組卷：24引用：2難度：0.7

  解析

• 6．我國人臉識別技術(shù)處于世界領(lǐng)先地位．所謂人臉識別，就是利用計算機檢測樣本之間的相似度，余弦距離是檢測相似度的常用方法．假設(shè)二維空間中有兩個點A（x₁，y₁），B（x₂，y₂），O為坐標原點，余弦相似度Similarity為向量

  OA

  ，

  OB

  夾角的余弦值，記作cos（A，B），余弦距離為1-cos（A，B）．已知P（cosα，sinα），Q（cosβ，sinβ），R（cosα，-sinα），若P、Q的余弦距離為

  1

  3

  ，

  Q

  ，

  R

  的余弦距離為

  1

  2

  ，則tanα?tanβ=（　　）

  A． 1 7

  B． 1 4

  C．4

  D．7
  組卷：42引用：2難度：0.6

  解析

• 7．直角梯形ABCD，滿足AB⊥AD，CD⊥AD，AB=2AD=2CD=2現(xiàn)將其沿AC折疊成三棱錐D-ABC，當三棱錐D-ABC體積取最大值時其外接球的體積為（　　）

  A． 3 π 2

  B． 4 3 π

  C．3π

  D．4π
  組卷：395引用：6難度：0.9

  解析

四、解答題：本大題共6小題，滿分70分.解答時要求寫出必要的文字說明、證明過程或推演步驟.

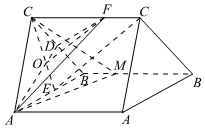• 21．如圖，直三棱柱ABC-A₁B₁C₁中，D、E分別是棱BC、AB的中點，點F在棱CC₁上，已知AB=AC，AA₁=3，BC=CF=2．
  （1）求證：C₁E∥平面ADF；
  （2）若點M在棱BB₁上，當BM為何值時，平面CAM⊥平面ADF？
  組卷：721引用：19難度：0.5

  解析

• 22．已知向量

  a

  =

  （

  cosωx

  ,

  sinωx

  ）

  （

  ω

  ＞

  0

  ）

  ，

  b

  =

  （

  1

  2

  ，

  3

  2

  ）

  ，

  f

  （

  x

  ）

  =

  a

  ?

  b

  ．
  （1）當

  x

  =

  π

  6

  時，函數(shù)f（x）取得最大值，求ω的最小值及此時f（x）的解析式；
  （2）現(xiàn)將函數(shù)f（x）的圖象沿x軸向左平移

  π

  3

  ω

  個單位，得到函數(shù)g（x）的圖象．已知A，B，C是函數(shù)f（x）與g（x）圖象上連續(xù)相鄰的三個交點，若△ABC是銳角三角形，求ω的取值范圍．
  組卷：72引用：4難度：0.5

  解析