當前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年重慶巴南區(qū)重慶實驗中學(xué)高三（上）期中數(shù)學(xué)試卷

發(fā)布：2024/9/30 0:0:1

一、單項選擇題：共8小題，每小題5分，共40分。

1．已知集合A={x||x-2|＜1}，B={x|log₂x＜1}，則A∪B=（　　）
A．（0，3） B．（1，2） C．（-∞，3） D．（0，2）
組卷：25引用：3難度：0.9
解析
2．已知復(fù)數(shù)z滿足
3
z
+
z
+
2
=
0
，則
|
3
z
|
=（　　）
A．3 B．1 C．
3
3
D．
3
組卷：243引用：2難度：0.5
解析
3．已知
2
sinα
=
3
+
2
3
cosα
，則
sin
（
2
α
-
π
6
）
=（　　）
A．
-
1
8
B．
-
7
8
C．
3
4
D．
7
8
組卷：481引用：6難度：0.5
解析
4．已知等比數(shù)列{a_n}的首項a₁=2，前n項和為S_n，且a₁，2a₂，4a₃成等差數(shù)列，則（　　）
A．
S
n
+
1
=
3
2
S
n
B．
S
n
+
1
=
1
2
S
n
+
2
C．S_n+1=a_n+1 D．
S
n
+
1
=
1
2
a
n
+
1
組卷：76引用：6難度：0.7
解析
5．已知四棱錐P-ABCD的底面是正方形，PA⊥平面ABCD，若PA=2AB，則平面ABP與平面CDP夾角的余弦值為（　　）
A．
1
3
B．
2
5
5
C．
5
5
D．
3
3
組卷：67引用：4難度：0.7
解析
6．某款對戰(zhàn)游戲，總有一定比例的玩家作弊該游戲每10個人組成一組對局，若一組對局中有作弊玩家，則認為這組對局不公平．現(xiàn)有50名玩家，其中有2名玩家為作弊玩家，一次性將50名玩家平均分為5組，則5組對局中，恰有一組對局為不公平對局的概率為（　　）
A．
7
20
B．
1
6
C．
9
49
D．
1
5
組卷：25引用：4難度：0.7
解析
7．設(shè)函數(shù)
f
（
x
）
=
（
e
x
-
a
）
2
16
+
（
x
-
a
）
2
（
x
∈
R
）
，若關(guān)于x的不等式
f
（
x
）
≤
1
17
有解，則實數(shù)a的值為（　　）
A．
1
5
B．
1
10
C．
1
17
D．
1
18
組卷：42引用：6難度：0.3
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題：共70分。

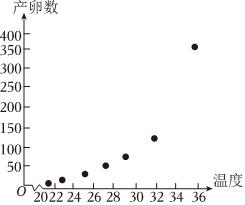21．紅蜘蛛是柚子的主要害蟲之一，能對柚子樹造成嚴重傷害，每只紅蜘蛛的平均產(chǎn)卵數(shù)y（個）和平均溫度x（℃）有關(guān)，現(xiàn)收集了以往某地的7組數(shù)據(jù)，得到下面的散點圖及一些統(tǒng)計量的值．

參考數(shù)據(jù)（z=lny）

7
∑
i
=
1
x
2
i

7
∑
i
=
1
x
i
y
i

7
∑
i
=
1
x
i
z
i

x

y

z

5215 17713 714 27 81.3 3.6

（1）根據(jù)散點圖判斷，y=bx+a與y=ce^dx（其中e=2.718…為自然對數(shù)的底數(shù)）哪一個更適合作為平均產(chǎn)卵數(shù)y（個）關(guān)于平均溫度x（℃）的回歸方程類型？（給出判斷即可，不必說明理由）
（2）由（1）的判斷結(jié)果及表中數(shù)據(jù)，求出y關(guān)于x的回歸方程．（計算結(jié)果精確到0.1）
附：回歸方程
?
y
=
?
b
x
+
?
a
，
?
b
=
n
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）
n
∑
i
=
1
（
x
i
-
x
）
2
=
n
∑
i
=
1
x
i
y
i
-
n
x
y
n
∑
i
=
1
x
2
i
-
n
x
2
，
?
a
=
y
-
?
b
x

（3）根據(jù)以往每年平均氣溫以及對果園年產(chǎn)值的統(tǒng)計，得到以下數(shù)據(jù)：平均氣溫在22℃以下的年數(shù)占60%，對柚子產(chǎn)量影響不大，不需要采取防蟲措施；平均氣溫在22℃至28℃的年數(shù)占30%，柚子產(chǎn)量會下降20%；平均氣溫在28℃以上的年數(shù)占10%，柚子產(chǎn)量會下降50%．為了更好的防治紅蜘蛛蟲害，農(nóng)科所研發(fā)出各種防害措施供果農(nóng)選擇．
在每年價格不變，無蟲害的情況下，某果園年產(chǎn)值為200萬元，根據(jù)以上數(shù)據(jù)，以得到最高收益（收益=產(chǎn)值-防害費用）為目標，請為果農(nóng)從以下幾個方案中推薦最佳防害方案，并說明理由．
方案1：選擇防害措施A，可以防止各種氣溫的紅蜘蛛蟲害不減產(chǎn)，費用是18萬；
方案2：選擇防害措施B，可以防治22℃至28℃的蜘蛛蟲害，但無法防治28℃以上的紅蜘蛛蟲害，費用是10萬；
方案3：不采取防蟲害措施．

組卷：232引用：2難度：0.6

解析

22．已知函數(shù)
f
（
x
）
=
ln
（
1
+
x
）
+
x
2
2
．
（1）當x∈[0，+∞）時，比較f（x）與x的大小；
（2）若函數(shù)
g
（
x
）
=
cosx
+
x
2
2
，且
f
（
e
a
2
）
=
g
（
b
）
-
1
（
a
＞
0
，
b
＞
0
）
，證明：f（b²）+1＞g（a+1）．
組卷：63引用：12難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業(yè) 發(fā)布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費下載

A． S n + 1 = 3 2 S n	B． S n + 1 = 1 2 S n + 2
C．S_n+1=a_n+1	D． S n + 1 = 1 2 a n + 1

參考數(shù)據(jù)（z=lny）
7 ∑ i = 1 x 2 i	7 ∑ i = 1 x i y i	7 ∑ i = 1 x i z i	x	y	z
5215	17713	714	27	81.3	3.6

2023-2024學(xué)年重慶巴南區(qū)重慶實驗中學(xué)高三（上）期中數(shù)學(xué)試卷

一、單項選擇題：共8小題，每小題5分，共40分。

1．已知集合A={x||x-2|＜1}，B={x|log2x＜1}，則A∪B=（ ）

2．已知復(fù)數(shù)z滿足3z+z+2=0，則|3z|=（ ）

3．已知2sinα=3+23cosα，則sin（2α-π6）=（ ）

4．已知等比數(shù)列{an}的首項a1=2，前n項和為Sn，且a1，2a2，4a3成等差數(shù)列，則（ ）

5．已知四棱錐P-ABCD的底面是正方形，PA⊥平面ABCD，若PA=2AB，則平面ABP與平面CDP夾角的余弦值為（ ）

7．設(shè)函數(shù)f（x）=（ex-a）216+（x-a）2（x∈R），若關(guān)于x的不等式f（x）≤117有解，則實數(shù)a的值為（ ）

四、解答題：共70分。

22．已知函數(shù)f（x）=ln（1+x）+x22．（1）當x∈[0，+∞）時，比較f（x）與x的大小；（2）若函數(shù)g（x）=cosx+x22，且f（ea2）=g（b）-1（a＞0，b＞0），證明：f（b2）+1＞g（a+1）．

1．已知集合A={x||x-2|＜1}，B={x|log₂x＜1}，則A∪B=（　　）

2．已知復(fù)數(shù)z滿足
3
z
+
z
+
2
=
0
，則
|
3
z
|
=（　　）

3．已知
2
sinα
=
3
+
2
3
cosα
，則
sin
（
2
α
-
π
6
）
=（　　）

4．已知等比數(shù)列{a_n}的首項a₁=2，前n項和為S_n，且a₁，2a₂，4a₃成等差數(shù)列，則（　　）

5．已知四棱錐P-ABCD的底面是正方形，PA⊥平面ABCD，若PA=2AB，則平面ABP與平面CDP夾角的余弦值為（　　）

7．設(shè)函數(shù)
f
（
x
）
=
（
e
x
-
a
）
2
16
+
（
x
-
a
）
2
（
x
∈
R
）
，若關(guān)于x的不等式
f
（
x
）
≤
1
17
有解，則實數(shù)a的值為（　　）

22．已知函數(shù)
f
（
x
）
=
ln
（
1
+
x
）
+
x
2
2
．
（1）當x∈[0，+∞）時，比較f（x）與x的大小；
（2）若函數(shù)
g
（
x
）
=
cosx
+
x
2
2
，且
f
（
e
a
2
）
=
g
（
b
）
-
1
（
a
＞
0
，
b
＞
0
）
，證明：f（b²）+1＞g（a+1）．