2022-2023學(xué)年甘肅省蘭州市教育局第四片區(qū)高一(下)期末數(shù)學(xué)試卷
發(fā)布:2024/6/2 8:0:8
一、單項(xiàng)選擇題:(本題共9小題,每小題4分,共36分,每小題只有一個(gè)正確選項(xiàng).)
-
1.|2+i2+2i3|=( )
A.1 B.2 C. 5D.5 組卷:2330引用:5難度:0.7 -
2.正方形ABCD的邊長(zhǎng)是2,E是AB的中點(diǎn),則
?EC=( )EDA. 5B.3 C.2 5D.5 組卷:175引用:13難度:0.7 -
3.如圖所示的糧倉(cāng)可以看成圓柱體與圓錐體的組合體,設(shè)圓錐部分的高為0.5米,圓柱部分的高為2米,底面圓的半徑為1米,則該組合體體積為( )
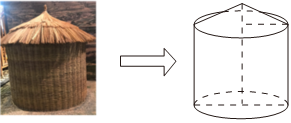
A. 立方米π3B.2π立方米 C. 立方米13π6D. 立方米5π2組卷:176引用:8難度:0.7 -
4.等邊三角形ABC中,
( )AB與BC的夾角為A.60° B.-60° C.120° D.150° 組卷:125引用:5難度:0.9 -
5.長(zhǎng)方體的一個(gè)頂點(diǎn)上的三條棱長(zhǎng)分別是3、4、5,且它的8個(gè)頂點(diǎn)都在同一球面上,則這個(gè)球的表面積是( )
A.25π B.50π C.100π D.200π 組卷:157引用:3難度:0.7 -
6.在長(zhǎng)方體ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E為CC1的中點(diǎn),則異面直線BC1與AE所成角的余弦值為( )
A. 155B. 105C.0 D. 63組卷:165引用:3難度:0.5
四、解答題:(本題共4小題,共36分.解答時(shí),應(yīng)寫出必要的文字說(shuō)明、證明過(guò)程或演算步驟.)
-
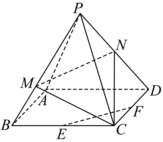 19.如圖,在正四棱錐P-ABCD中AB=2,PA=4,,N、E、F分別為PD、BC、CD中點(diǎn).PM=2MB
19.如圖,在正四棱錐P-ABCD中AB=2,PA=4,,N、E、F分別為PD、BC、CD中點(diǎn).PM=2MB
(1)求證:EF∥平面PMN;
(2)三棱錐N-MCD的體積.組卷:72引用:3難度:0.5 -
20.已知點(diǎn)P(
,1),Q(cosx,sinx),O為坐標(biāo)原點(diǎn),函數(shù)f(x)=3?OP.QP
(Ⅰ)求函數(shù)f(x)的解析式及f(x)的最小正周期;
(Ⅱ)若A為△ABC的內(nèi)角,f(A)=4,BC=3,求△ABC周長(zhǎng)的最大值.組卷:322引用:5難度:0.5


