2011年人教A版模塊考試數學試卷1(必修4)
發布:2024/11/1 21:0:2
一、選擇題(共12小題,每小題5分,滿分60分)
-
1.下列命題正確的是( )
A.第一象限角是銳角 B.鈍角是第二象限角 C.終邊相同的角一定相等 D.不相等的角,它們終邊必不相同 組卷:766引用:14難度:0.9 -
2.在四邊形ABCD中,如果
,AB?AD=0,那么四邊形ABCD的形狀是( )AB=DCA.矩形 B.菱形 C.正方形 D.直角梯形 組卷:42引用:7難度:0.9 -
3.與向量
=(12,5)平行的單位向量為( )aA. (1213,-513)B. (-1213,-513)C. 或(1213,513)(-1213,-513)D. 或(-1213,513)(1213,-513)組卷:675引用:18難度:0.9 -
4.已知
,|a|=2sin15°,|b|=4cos15°,則<a,b>=30°的值為( )a?bA. 3B. 23C.3 D.1 組卷:36引用:9難度:0.9 -
5.下列函數中,在區間
上為增函數且以π為周期的函數是( )(0,π2)A. y=sinx2B.y=sinx C.y=-tanx D.y=-cos2x 組卷:130引用:39難度:0.9 -
6.在△ABC中,∠C=120°,
,則tanAtanB的值為( )tanA+tanB=233A. 14B. 13C. 12D. 53組卷:476引用:24難度:0.9 -
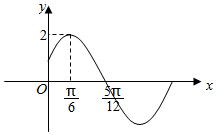 7.已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分圖象如圖所示,則函數f(x)的解析式為( )π2
7.已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分圖象如圖所示,則函數f(x)的解析式為( )π2A. f(x)=2sin(12x+π6)B. f(x)=2sin(12x-π6)C. f(x)=2sin(2x-π6)D. f(x)=2sin(2x+π6)組卷:517引用:32難度:0.9
三、解答題(共6小題,滿分74分)
-
21.已知函數f(x)=sin(ωx+?)(ω>0,0≤?≤π)為偶函數,其圖象上相鄰的兩個最高點之間的距離為2π.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若,求α∈(-π3,π2),f(α+π3)=13的值.sin(2α+5π3)組卷:239引用:28難度:0.1 -
22.設函數
(x∈R),其中t∈R,將f(x)的最小值記為g(t).f(x)=-cos2x-4t?sinx2cosx2+2t2-6t+2
(1)求g(t)的表達式;
(2)當-1≤t≤1時,要使關于t的方程g(t)=kt有且僅有一個實根,求實數k的取值范圍組卷:101引用:6難度:0.5


