2022-2023學年山東省泰安市新泰市八年級（下）期末數學試卷（五四學制）

一、選擇題（本大題共12小題，在每小題給出的四個選項中，只有一個是正確的，請把正確的選項選出來，每小題選對得4分，選錯、不選或選出的答案超過一個，均記零分）

• 1．下列計算正確的是（　　）

  A． 16 =± 4	B． （ - 2 ） 2 × 3 = - 2 3
  C． 3 - 8 = 2	D． - 64 = - 8
  組卷：99引用：2難度：0.7

  解析

• 2．已知

  m

  n

  =

  2

  3

  ，則

  m

  m

  +

  n

  的值為（　　）

  A． 3 5

  B． 2 5

  C． 7 5

  D． 2 3
  組卷：1117引用：12難度：0.8

  解析

• 3．如圖，為估算某河的寬度，在河對岸選定一個目標點A，在近岸取B，C，D三點，使得AB⊥BC，CD⊥BC，點E在BC上，并且點A，E，D在同一條直線上，若測得BE=20m,CE=10m,CD=20m,則河的寬度為（　　）

  A．20m

  B．30m

  C．40m

  D．60m
  組卷：851引用：8難度：0.5

  解析

• 4．方程x²-2x-1=0根的情況是（　　）

  A．有兩個相等的實數根	B．只有一個實數根
  C．沒有實數根	D．有兩個不相等的實數根
  組卷：466引用：12難度：0.9

  解析

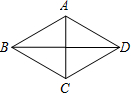• 5．如圖，四邊形ABCD的對角線AC、BD互相垂直，則下列條件能判定四邊形ABCD為菱形的是（　　）

  A．BA=BC	B．AC、BD互相平分
  C．AC=BD	D．AB∥CD
  組卷：873引用：39難度：0.9

  解析

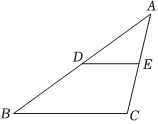• 6．如圖，已知△ADE與△ABC的相似比為1：2，則△ADE與四邊形BCED的面積比為（　　）

  A．1：2

  B．1：3

  C．1：4

  D．3：4
  組卷：150引用：3難度：0.9

  解析

• 7．《九章算術》是中國傳統數學重要的著作之一，奠定了中國傳統數學的基本框架．書中有一題“今有戶高多于廣六尺八寸，兩隅相去適一丈，問戶高，廣各幾何？”其大意是：“已知長方形門的高比寬多6尺8寸，門的對角線長1丈，那么門的高和寬各是多少？”若設寬為x尺，則可列方程為（　　）

  A．x2+（x-6.8）2=100	B．x（x+6.8）=100
  C．x2+（x+6.8）2=100	D．x（x-6.8）2=100
  組卷：447引用：6難度：0.6

  解析

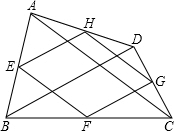• 8．如圖，點E、F、G、H分別是四邊形ABCD邊AB、BC、CD、DA的中點．則下列說法：
  ①若AC=BD，則四邊形EFGH為矩形；
  ②若AC⊥BD，則四邊形EFGH為菱形；
  ③若四邊形EFGH是平行四邊形，則AC與BD互相平分；
  ④若四邊形EFGH是正方形，則AC與BD互相垂直且相等．
  其中正確的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：3446引用：42難度：0.7

  解析

三、解答題（本大題共7小題，滿分78分，解答應寫出必要的文字說明、證明過程或推演步驟）

• 24．某商城在2021年端午節期間促銷海爾冰箱，每臺進貨價為2500元，標價為3000元．
  （1）商城舉行了“新老用戶粽是情”摸獎活動，中獎者商城將冰箱連續兩次降價，每次降價的百分率相同，最后以2430元售出，求每次降價的百分率；
  （2）市場調研表明：當每臺售價為2900元時，平均每天能售出8臺，當每臺售價每降50元時，平均每天就能多售出4臺，若商城要想使海爾冰箱的銷售利潤平均每天達到5000元，則每臺冰箱的定價應為多少元？
  組卷：4956引用：12難度：0.7

  解析

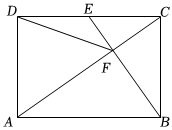• 25．如圖，在矩形ABCD中，E是CD邊的中點，且BE⊥AC于點F，連接DF．
  求證：（1）AD=DF；
  （2）DF²=BE?BF．
  ?
  組卷：688引用：3難度：0.5

  解析