2023-2024學年四川省成都七中高三（上）零診數學試卷（理科）

一、單選題：共12道小題，每題5分，共60分.

• 1．設

  z

  =

  1

  -

  i

  1

  +

  i

  +

  2

  i

  ，則z的虛部為（　　）

  A．i

  B．3i

  C．1

  D．3
  組卷：68引用：6難度：0.8

  解析

• 2．直線l₁：x+ay-1=0與直線l₂：ax+y+1=0平行，則a=（　　）

  A．0

  B．1

  C．-1

  D．1或-1
  組卷：156引用：4難度：0.8

  解析

• 3．一組數據包括47、48、51、54、55，則這組數據的標準差為（　　）

  A． 10

  B． 5 2

  C．10

  D．50
  組卷：98引用：3難度：0.9

  解析

• 4．已知函數f（x）在其定義域R上的導函數為f′（x），當x∈R時，f′（x）＞0是“f（x）單調遞增”的（　　）

  A．充要條件	B．既不充分也不必要條件
  C．必要不充分條件	D．充分不必要條件
  組卷：77引用：4難度：0.8

  解析

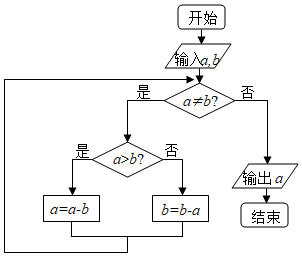• 5．如圖所示的算法框圖思路源于我國古代數學名著《九章算術》中的“更相減相術”，執行該算法框圖，若輸入的a、b分別為36、96，則輸出的a=（　　）

  A．0

  B．8

  C．12

  D．24
  組卷：127引用：7難度：0.7

  解析

• 6．直線x=2與拋物線C：y²=2px（p＞0）交于D、E兩點，若

  OD

  ?

  OE

  =

  0

  ，其中O為坐標原點，則C的準線方程為（　　）

  A． x = - 1 4

  B． x = - 1 2

  C．x=-1

  D．x=-2
  組卷：68引用：4難度：0.7

  解析

• 7．函數y=lgx的圖象經過變換

  φ

  ：

  x ′ = 10 x

  y ′ = y + 2

  后得到函數y′=f（x′）的圖象，則f（x）=（　　）

  A．-1+lgx

  B．1+lgx

  C．-3+lgx

  D．3+lgx
  組卷：16引用：2難度：0.7

  解析

三、解答題：共5道大題，共70分.

• 21．設函數f（x）=e^x-ax,其中a∈R．
  （1）討論函數f（x）在[1，+∞）上的極值；
  （2）若函數f（x）有兩零點x₁，x₂（x₁＜x₂），且滿足

  x

  1

  +

  λ

  x

  2

  1

  +

  λ

  ＞

  1

  ，求正實數λ的取值范圍．
  組卷：83引用：4難度：0.5

  解析

• 22．在平面直角坐標系xOy中，以O為極點，x軸的正半軸為極軸，建立極坐標系，曲線C和直線l的極坐標方程分別為ρ=2sinθ+2acosθ和

  ρsin

  （

  x

  -

  π

  4

  ）

  =

  2

  ．且二者交于M，N兩個不同點．
  （1）寫出曲線C和直線l的直角坐標方程；
  （2）若點P的極坐標為（2，π），|PM|+|PN|=5

  2

  ，求a的值．
  組卷：50引用：2難度：0.6

  解析