蘇教版（2019）必修第一冊 《第7章 三角函數》2020年單元測試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．下列函數中，最小正周期為π的函數是（　　）

  A．y=sinx	B．y=cosx
  C．y=sin（ 1 2 x+ π 3 ）	D．y=cos（ π 3 -2x）
  組卷：81引用：1難度：0.8

  解析

• 2．已知點P（3，4）在角α的終邊上，則

  cos

  （

  π

  2

  +

  α

  ）

  的值為（　　）

  A． 3 5

  B． - 3 5

  C． 4 5

  D． - 4 5
  組卷：627引用：7難度：0.8

  解析

• 3．代數式sin（-330°）cos390°的值為（　　）

  A．- 3 4

  B． 3 4

  C．- 3 4

  D． 1 4
  組卷：62引用：1難度：0.8

  解析

• 4．已知tan（

  π

  3

  -α）=

  1

  3

  ，則tan（

  2

  π

  3

  +α）=（　　）

  A． 1 3

  B．- 1 3

  C． 2 3 3

  D．- 2 3 3
  組卷：58引用：4難度：0.9

  解析

• 5．函數y=2^|x|sin2x的圖象可能是（　　）

  A．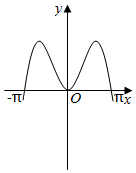

  B．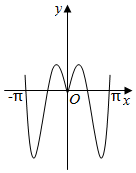

  C．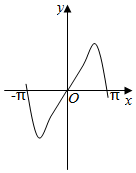

  D．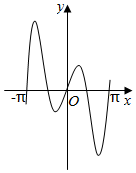
  組卷：8051引用：113難度：0.7

  解析

• 6．若A為三角形ABC的一個內角，且sinA+cosA=

  2

  3

  ，則這個三角形是（　　）

  A．鈍角三角形

  B．直角三角形

  C．銳角三角形

  D．正三角形
  組卷：316引用：7難度：0.9

  解析

• 7．下列函數中，以

  π

  2

  為最小正周期且在區間（

  π

  4

  ，

  π

  2

  ）單調遞增的是（　　）

  A．f（x）=|cos2x|

  B．f（x）=|sin2x|

  C．f（x）=cos|x|

  D．f（x）=sin|x|
  組卷：3118引用：18難度：0.6

  解析

四、解答題（本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟）

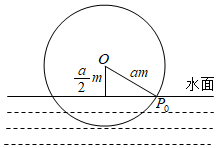• 21．設a為正實數．如圖，一個水輪的半徑為am,水輪圓心O距離水面

  a

  2

  m

  ，已知水輪每分鐘逆時針轉動5圈．當水輪上的點P從水中浮現時（即圖中點P₀）開始計算時間．
  （1）將點P距離水面的高度h（m）表示為時間t（s）的函數；
  （2）點P第一次達到最高點需要多少時間．
  組卷：312引用：2難度：0.6

  解析

• 22．已知函數f（x）=Asin（ωx+φ）+B（A＞0，ω＞0）的一系列對應值如表：

  x	- π 6	π 3	5 π 6	4 π 3	11 π 6	7 π 3	17 π 6
  y	-1	1	3	1	-1	1	3

  （1）根據表格提供的數據求函數f（x）的一個解析式．
  （2）根據（1）的結果，若函數y=f（kx）（k＞0）周期為

  2

  π

  3

  ，當

  x

  ∈

  [

  0

  ，

  π

  3

  ]

  時，方程f（kx）=m恰有兩個不同的解，求實數m的取值范圍．
  組卷：653引用：51難度：0.7

  解析