2022-2023學年湖南省婁底市漣源二中、漣源一中、婁底三中等名校高一（下）期末數學試卷

一、選擇題：本大題共8小題：每小題5分，共40分．在每小題給出的四個選項中，只有一個選項是符合題目要求的．

• 1．若（z+3i）（3+i）=1+2i,則復數z的共軛復數是（　　）

  A． 1 2 - 5 2 i

  B．1-2i

  C． 1 2 + 5 2 i

  D．2+i
  組卷：47引用：3難度：0.7

  解析

• 2．在△ABC中，角A，B，C所對的邊分別是a,b,c,a=

  6

  ，b=2，A=

  π

  4

  ，則sinB=（　　）

  A． 3 3

  B． - 3 3

  C． 6 3

  D． - 6 3
  組卷：342引用：7難度：0.8

  解析

• 3．甲乙兩個雷達獨立工作，它們發現飛行目標的概率分別是0.9和0.8，飛行目標被雷達發現的概率為（　　）

  A．0.72

  B．0.26

  C．0.7

  D．0.98
  組卷：403引用：5難度：0.7

  解析

• 4．已知向量

  a

  =

  （

  1

  ，

  1

  ）

  ，

  a

  ?

  b

  =

  6

  ，

  |

  b

  |

  =

  2

  ，則向量

  a

  ，

  b

  的夾角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  組卷：317引用：7難度：0.7

  解析

• 5．已知某圓錐的側面積為

  5

  π

  ，該圓錐側面的展開圖是弧長為2π的扇形，則該圓錐的體積為（　　）

  A． π 3

  B． 2 π 3

  C．π

  D．2π
  組卷：95引用：4難度：0.7

  解析

• 6．在△ABC在中，點D線段BC上任意一點，點D滿足

  AD

  =

  3

  AP

  ，若存在實數m和n,使得

  BP

  =

  m

  AB

  +

  n

  AC

  ，則m+n=（　　）

  A． 2 3

  B． 1 3

  C． - 1 3

  D． - 2 3
  組卷：200引用：6難度：0.7

  解析

• 7．在矩形ABCD中，AB=1，

  AD

  =

  3

  ，沿對角線AC將矩形折成一個直二面角B-AC-D，則點B與點D之間的距離為（　　）

  A． 3

  B． 5

  C． 7 2

  D． 10 2
  組卷：83引用：3難度：0.7

  解析

四、解答題：本大題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．甲、乙兩位射手對同一目標各射擊兩次，且每人每次擊中目標與否均互不影響．已知甲每次擊中目標的概率為

  2

  3

  ，乙每次擊中目標的概率為

  3

  4

  ．
  （Ⅰ）求甲兩次都沒有擊中目標的概率；
  （Ⅱ）在四次射擊中，求甲、乙恰好各擊中一次目標的概率．
  組卷：295引用：4難度：0.7

  解析

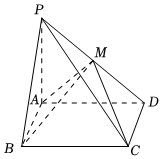• 22．如圖，在四棱錐P-ABCD中，底面ABCD是矩形，PA=AD=4，AB=2，PA⊥平面ABCD，且M是PD的中點．
  （1）求證：AM⊥平面PCD；
  （2）求異面直線CD與BM所成角的正切值；
  （3）求直線CD與平面ACM所成角的正弦值．
  組卷：1257引用：11難度：0.6

  解析