2014-2015學年江蘇省宿遷市沭陽縣銀河學校高三（上）開學數學試卷

一、填空題：本大題共14小題，每小題5分，共70分．

• 1．函數f（x）=sin（ωx-

  π

  3

  ）的最小正周期為

  π

  3

  ，其中ω＞0，則ω=

  ．
  組卷：29引用：2難度：0.9

  解析

• 2．若復數z=a²-1+（a+1）i（a∈R）為純虛數，則a=

  ．
  組卷：159引用：4難度：0.9

  解析

• 3．若A={x∈Z|2≤2^x≤16}，B={3，4，5}，則A∩B=

   

  ．
  組卷：25引用：3難度：0.9

  解析

• 4．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）中，若以其焦點為圓心，半實軸長為半徑的圓與漸近線相切，則其漸近線方程為

   

  ．
  組卷：69引用：3難度：0.9

  解析

• 5．如果數據x₁，x₂，x₃，…，x_n的方差是a,若數據3x₁-2，3x₂-2，3x₃-2，…，3x_n-2的方差為9，則a=

   

  ．
  組卷：67引用：4難度：0.7

  解析

• 6．執行如圖所示程序框圖，若p=80，則輸出的n的值為

  ．
  
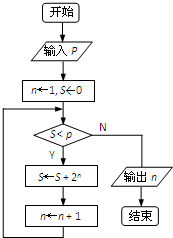  組卷：45引用：3難度：0.7

  解析

• 7．如果投擲兩顆骰子，得到其向上的點數分別為x和y,則log_x（y-1）=1的概率為

   

  ．
  組卷：44引用：3難度：0.7

  解析

• 8．若f（x）是R上的增函數，且f（-1）=-4，f（2）=2，設P={x|f（x+t）＜2}，Q={x|f（x）＜-4}，若“x∈P”是“x∈Q”的充分不必要條件，則實數t的取值范圍是

  ．
  組卷：56引用：10難度：0.7

  解析

七、【必做題】第25題、第26題，每題10分，共計20分.

• 25．在如圖所示的幾何體中，四邊形ABCD為矩形，平面ABEF⊥平面ABCD，EF∥AB，∠BAF=90°，AD=2，AB=AF=2EF=1，點P在棱DF上．
  （Ⅰ）求證：AD⊥BF：
  （Ⅱ）若P是DF的中點，求異面直線BE與CP所成角的余弦值；
  （Ⅲ）若二面角D-AP-C的余弦值為

  6

  3

  ，求PF的長度．
  組卷：238引用：11難度：0.1

  解析

• 26．數列{a_n}滿足a_n+1=2a_n²-1，a_N=1且a_N-1≠1，其中N∈{2，3，4，…}
  （1）求證：|a₁|≤1；
  （2）求證：a₁=cos

  kπ

  2

  N

  -

  2

  （k∈Z）．
  組卷：32引用：2難度：0.3

  解析