2023-2024學年北京市門頭溝區大峪中學高二（上）期中數學試卷

一、選擇題（本大題共10小題，每題4分，共40分）

• 1．已知直線

  l

  ：

  3

  x

  -

  y

  -

  4

  =

  0

  ，則直線l的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：195引用：5難度：0.8

  解析

• 2．已知空間向量

  a

  =

  （

  0

  ，

  2

  ，

  0

  ）

  ，

  b

  =

  （

  1

  ，

  0

  ，-

  1

  ）

  ，則

  （

  a

  +

  b

  ）

  ?

  b

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：65引用：3難度：0.8

  解析

• 3．圓x²+y²-2x+4y+1=0與圓（x-4）²+（y-2）²=16的位置關系為（　　）

  A．相離

  B．外切

  C．相交

  D．內切
  組卷：82引用：3難度：0.7

  解析

• 4．若x²+y²-4x-2y+m=0表示圓的方程，則m的取值范圍是（　　）

  A．（-∞，5）

  B．（-∞，5]

  C．（5，+∞）

  D．[5，+∞）
  組卷：91引用：3難度：0.9

  解析

• 5．已知直線x+ay-1=0和直線ax+4y+2=0互相平行，則a的值是（　　）

  A．0

  B．2

  C．-2

  D．±2
  組卷：106引用：4難度：0.7

  解析

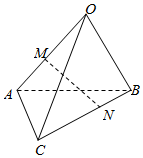• 6．如圖，空間四邊形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M是OA的中點，點N在BC上，且

  CN

  =2

  NB

  ，設

  MN

  =x

  a

  +y

  b

  +z

  c

  ，則x,y,z的值為（　　）

  A． 1 2 ， 1 3 ， 2 3

  B． 1 2 ， 2 3 ， 1 3

  C．- 1 2 ， 2 3 ， 1 3

  D．- 1 2 ， 1 3 ， 2 3
  組卷：617引用：21難度：0.8

  解析

• 7．點（-1，2）關于直線x+y+4=0的對稱點的坐標為（　　）

  A．（-6，-3）

  B．（-3，-6）

  C．（-7，-2）

  D．（-2，-7）
  組卷：137引用：2難度：0.7

  解析

三、解答題（共6小題，共85分.解答應寫出文字說明、證明過程或演算步驟）

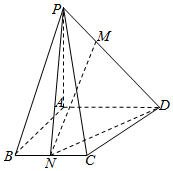• 20．如圖，在四棱錐P-ABCD中，底面ABCD為直角梯形，其中AD∥BC，AD⊥BA，AD=3，AB=BC=2，PA⊥平面ABCD，且PA=3，點M在棱PD上，點N為BC中點．
  （1）證明：若DM=2MP，直線MN∥平面PAB；
  （2）求二面角C-PD-N的正弦值；
  （3）是否存在點M，使NM與平面PCD所成角的正弦值為

  2

  6

  ？若存在求出

  PM

  PD

  值；若不存在，說明理由．
  組卷：603引用：10難度：0.6

  解析

• 21．對于平面直角坐標系中的兩點A（x₁，y₁），B（x₂，y₂），現定義由點A到點B的“折線距離”ρ（A，B）為ρ（A，B）=|x₂-x₁|+|y₂-y₁|．
  （1）已知A（1，0），B（2，3），求ρ（A，B）；
  （2）已知點A（1，0），點B是直線

  l

  ：

  x

  -

  2

  y

  +

  2

  =

  0

  上的一個動點，求ρ（A，B）的最小值；
  （3）對平面上給定的兩個不同的點A（x₁，y₁），B（x₂，y₂），是否存在點C（x,y），同時滿足
  ①ρ（A，C）+ρ（C，B）=ρ（A，B）；②ρ（A，C）=ρ（C，B）．
  若存在，請求出所有符合條件的點；若不存在，請予以證明．
  組卷：32引用：3難度：0.5

  解析