當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省深圳外國語學校高三（上）第一次月考數學試卷

發布：2024/7/16 8:0:9

一、單選題（本題共8小題，每小題5分，共40分．每小題給出的四個選項中，只有一個選項是符合題目要求的）

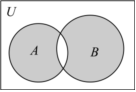1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，則圖中陰影部分表示的集合為（　　）
?
A．（-2，0] B．[-2，0] C．[-2，0]∪{4} D．（-2，0]∪{4}
組卷：454引用：6難度：0.8
解析
2．若復數z所對應的點在第四象限，且滿足z²-2z+2=0，則z²=（　　）
A．1+i B．1-i C．-2i D．2i
組卷：79引用：6難度：0.8
解析
3．已知
a
?
b
=
-
24
，
a
+
2
b
=
（
-
5
，
2
）
，若
a
與
b
模相等，則
|
a
|
=（　　）
A．3 B．4 C．5 D．6
組卷：308引用：4難度：0.7
解析
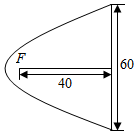4．探照燈反射鏡的縱斷面是拋物線的一部分，光源放在焦點F處．已知燈口直徑為60cm,光源距燈口的深度為40cm,則光源到反射鏡的頂點的距離為（　　）
A．5cm B．10cm C．15cm D．20cm
組卷：47引用：2難度：0.8
解析
5．設函數f（x）=（a-1）x|x-b+1|為奇函數且在R上為減函數，則關于a、b的值表述正確的是（　　）
A．a＞1，b=1 B．a＞1，b＜1 C．a＜1，b=1 D．a＜1，b＞1
組卷：81引用：2難度：0.8
解析
6．定義函數迭代：
f^（0）（x）=x
f^（1）（x）=f（x）
f^（2）（x）=f（f（x））
?
f^（n+1）（x）=f（f^（n）（x））
已知f（x）=3x+2，則f^（n）（x）=（　　）
A．3ⁿx+3ⁿ-1 B．3ⁿx+3ⁿ+1 C．3nx+3n-1 D．3ⁿx-3ⁿ+1
組卷：51引用：3難度：0.6
解析
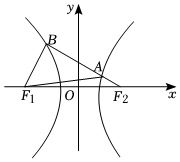7．如圖，F₁、F₂是雙曲線C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦點，過F₂的直線與雙曲線C交于A、B兩點．若A是BF₂中點且BF₁⊥BF₂，則該雙曲線的漸近線方程為（　　）
A．y=±2
3
x B．y=±2
2
x C．y=±
3
x D．y=±
2
x
組卷：574引用：7難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，共70分，其中17題10分，其余各題12分.解答應寫出文字說明、證明過程或演算步驟）

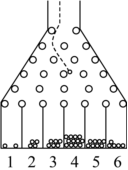21．高爾頓板又稱豆機、梅花機等，是英國生物統計學家高爾頓設計用來研究隨機現象的模型．如圖所示的高爾頓板為一塊木板自上而下釘著6層圓柱形小木塊，最頂層有2個小木塊，以下各層小木塊的個數依次遞增，各層小木塊互相平行但相互錯開，小木塊之間留有適當的空隙作為通道，前面擋有一塊透明玻璃．讓小球從高爾頓板上方的通道口落下，小球在下落過程中與層層小木塊碰撞，且等可能向左或者向右滾下，最后落入高爾頓板下方從左至右編號為1，2，…，6的球槽內．
（1）某商店將該高爾頓板改良成游戲機，針對某商品推出促銷活動．凡是入店購買該商品一件，就可以獲得一次游戲機會．若小球落入X號球槽，該商品可立減Y元，其中Y=|20-5X|．若該商品的成本價是10元，從期望的角度考慮，為保證該商品總體能盈利，求該商品的最低定價．（結果取整數）
（2）將79個小球依次從高爾頓板上方的通道口落下，試問3號球槽中落入多少個小球的概率最大？
附：設隨機變量ξ～B（n,p），則ξ的分布列為
P
（
ξ
=
k
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
，k=0，1，2，?，n.
P
（
ξ
=
k
）
P
（
ξ
=
k
-
1
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
C
k
-
1
n
p
k
-
1
（
1
-
p
）
n
-
k
+
1
=
1
+
（
n
+
1
）
p
-
k
k
（
1
-
p
）
．
組卷：146引用：5難度：0.5
解析
22．設函數f（x）=-xlnx+ax²+x（a∈R）．
（1）若函數f（x）有兩個不同的極值點，求實數a的取值范圍；
（2）若a=1，k∈N，g（x）=x²+2x,當x＞2時，不等式2k（x-2）+f（x）＜g（x）恒成立，試求k的最大值．
組卷：65引用：4難度：0.2
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2022-2023學年廣東省深圳外國語學校高三（上）第一次月考數學試卷

一、單選題（本題共8小題，每小題5分，共40分．每小題給出的四個選項中，只有一個選項是符合題目要求的）

1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，則圖中陰影部分表示的集合為（ ）?

2．若復數z所對應的點在第四象限，且滿足z2-2z+2=0，則z2=（ ）

3．已知a?b=-24，a+2b=（-5，2），若a與b模相等，則|a|=（ ）

4．探照燈反射鏡的縱斷面是拋物線的一部分，光源放在焦點F處．已知燈口直徑為60cm,光源距燈口的深度為40cm,則光源到反射鏡的頂點的距離為（ ）

5．設函數f（x）=（a-1）x|x-b+1|為奇函數且在R上為減函數，則關于a、b的值表述正確的是（ ）

6．定義函數迭代：f（0）（x）=xf（1）（x）=f（x）f（2）（x）=f（f（x））?f（n+1）（x）=f（f（n）（x））已知f（x）=3x+2，則f（n）（x）=（ ）

7．如圖，F1、F2是雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點，過F2的直線與雙曲線C交于A、B兩點．若A是BF2中點且BF1⊥BF2，則該雙曲線的漸近線方程為（ ）

四、解答題（本題共6小題，共70分，其中17題10分，其余各題12分.解答應寫出文字說明、證明過程或演算步驟）

22．設函數f（x）=-xlnx+ax2+x（a∈R）．（1）若函數f（x）有兩個不同的極值點，求實數a的取值范圍；（2）若a=1，k∈N，g（x）=x2+2x,當x＞2時，不等式2k（x-2）+f（x）＜g（x）恒成立，試求k的最大值．

1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，則圖中陰影部分表示的集合為（　　）
?

2．若復數z所對應的點在第四象限，且滿足z²-2z+2=0，則z²=（　　）

3．已知
a
?
b
=
-
24
，
a
+
2
b
=
（
-
5
，
2
）
，若
a
與
b
模相等，則
|
a
|
=（　　）

4．探照燈反射鏡的縱斷面是拋物線的一部分，光源放在焦點F處．已知燈口直徑為60cm,光源距燈口的深度為40cm,則光源到反射鏡的頂點的距離為（　　）

5．設函數f（x）=（a-1）x|x-b+1|為奇函數且在R上為減函數，則關于a、b的值表述正確的是（　　）

6．定義函數迭代：
f^（0）（x）=x
f^（1）（x）=f（x）
f^（2）（x）=f（f（x））
?
f^（n+1）（x）=f（f^（n）（x））
已知f（x）=3x+2，則f^（n）（x）=（　　）

7．如圖，F₁、F₂是雙曲線C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦點，過F₂的直線與雙曲線C交于A、B兩點．若A是BF₂中點且BF₁⊥BF₂，則該雙曲線的漸近線方程為（　　）

22．設函數f（x）=-xlnx+ax²+x（a∈R）．
（1）若函數f（x）有兩個不同的極值點，求實數a的取值范圍；
（2）若a=1，k∈N，g（x）=x²+2x,當x＞2時，不等式2k（x-2）+f（x）＜g（x）恒成立，試求k的最大值．