2022-2023學(xué)年浙江省麗水市縉云中學(xué)等四校高一（上）聯(lián)考數(shù)學(xué)試卷（12月份）

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知角α的頂點(diǎn)與原點(diǎn)O重合，始邊與x軸的非負(fù)半軸重合，它的終邊過點(diǎn)（-2，1），則sinα的值為（　　）

  A． - 5 5

  B． 5 5

  C． - 2 5 5

  D． 2 5 5
  組卷：12引用：4難度：0.8

  解析

• 2．已知全集U=R，集合

  A

  =

  {

  x

  |

  |

  x

  -

  1

  |

  ≤

  3

  }

  ，

  B

  =

  {

  x

  |

  x

  -

  5

  x

  +

  1

  ＜

  0

  }

  ，那么A∪B=（　　）

  A．（-1，4）

  B．（-1，4]

  C．（-2，5）

  D．[-2，5）
  組卷：18引用：3難度：0.7

  解析

• 3．下面命題中不正確的是（　　）

  A．“a＞1”是“ 1 a ＜ 1 ”的充分不必要條件

  B．命題“?x∈R，x2+x+1＜0”的否定是“?x∈R，x2+x+1≥0

  C．設(shè)x,y∈R，若“x+y≥4”則“x≥2且y≥2”是真命題

  D．設(shè)a,b∈R，則“a≠0且b≠0”是“ab≠0”的充要條件
  組卷：184引用：4難度：0.8

  解析

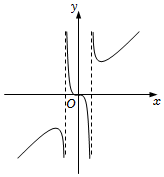• 4．函數(shù)f（x）的部分圖象如圖所示，則f（x）的解析式可能是（　　）

  A． f （ x ） = x 3 1 - | x |	B． f （ x ） = x x 2 + 1
  C． f （ x ） = x 3 x 2 - 1	D． f （ x ） = x 2 + 1 x 2 - 1
  組卷：231引用：8難度：0.7

  解析

• 5．已知a=sin

  5

  π

  6

  ，b=ln2，c=2 ^0.3，則a,b,c的大小關(guān)系為（　　）

  A．a(chǎn)＜b＜c

  B．c＜b＜a

  C．b＜a＜c

  D．a(chǎn)＜c＜b
  組卷：31引用：4難度：0.9

  解析

• 6．已知f（x）是定義在R上的增函數(shù)，且對(duì)任意x∈R，都有f（x₁）f（x₂）=f（x₁+x₂），則不等式

  f

  （

  x

  -

  2

  ）

  ＞

  [

  f

  （

  x

  +

  1

  2

  ）

  ]

  2

  的解集為（　　）

  A．（-3，+∞）

  B．（2，+∞）

  C．（-∞，-3）

  D．（-∞，2）
  組卷：42引用：3難度：0.5

  解析

• 7．若函數(shù)y=

  lo

  g

  1

  3

  （

  a

  x

  2

  -

  4

  x

  +

  12

  ）

  在區(qū)間[1，2]上單調(diào)遞增，則實(shí)數(shù)a的取值范圍（　　）

  A．（-1，1]

  B．[-1，1]

  C．（0，1]

  D．[0，1]
  組卷：239引用：5難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟

• 21．已知

  f

  （

  lo

  g

  2

  x

  ）

  =

  x

  -

  1

  x

  ．
  （1）求函數(shù)f（x）的表達(dá)式，并判斷函數(shù)f（x）的單調(diào)性（不需要證明）；
  （2）關(guān)于x的不等式4^1+x+4^1-x-8+3f（x）≥kf²（x）在[1，+∞）上有解，求實(shí)數(shù)k的取值范圍．
  組卷：181引用：3難度：0.6

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  |

  3

  x

  2

  -

  ax

  |

  +

  x

  2

  -

  x

  +

  1

  （

  x

  ＞

  0

  ）

  ，

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  x

  ．
  （1）若a=1，求f（x）的值域；
  （2）對(duì)任意x₀∈[3，4]，存在

  x

  1

  ，

  x

  2

  ∈

  [

  1

  8

  ，

  2

  ]

  （

  x

  1

  ≠

  x

  2

  ）

  ，使得x₀=g（x₁）=g（x₂），求實(shí)數(shù)a的取值范圍．
  組卷：29引用：3難度：0.4

  解析