當前位置：試卷中心 > 試卷詳情

2023-2024學年江西省宜春市豐城九中28、29班高三（上）開學數學試卷

發布：2024/8/29 1:0:9

一、單項選擇題：本題共8個小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．復數z滿足（z+1）i=1-i,則z的共軛復數的虛部是（　　）
A．1 B．-1 C．i D．-i
組卷：53引用：8難度：0.8
解析
2．已知集合A={x|4^x-2^x+1＜0}，B={x|y=lg（x+1）}，則A∩（?_RB）=（　　）
A．（-∞，-1] B．（-∞，1） C．（-1，1） D．（0，1）
組卷：23引用：3難度：0.8
解析
3．已知平面向量
a
=
（
2
5
5
，
5
5
）
，
b
為單位向量，且
（
a
+
2
b
）
⊥
（
a
-
b
）
，則向量
b
在向量
a
上的投影向量的坐標為（　　）
A．
（
-
2
5
5
，-
5
5
）
B．
（
2
5
5
，
5
5
）
C．
（
2
5
5
，-
5
5
）
D．
（
-
2
5
5
，
5
5
）
組卷：24引用：1難度：0.8
解析
4．設函數
f
（
x
）
=
2
x
2
-
ax
?
lg
x
-
1
x
+
1
為奇函數，則實數a的值為（　　）
A．-1 B．0 C．1 D．2
組卷：130引用：4難度：0.6
解析
5．已知A（0，-2），B（2，0），點P為圓x²+y²-2x-8y+13=0上任意一點，則△PAB面積的最大值為（　　）
A．5 B．
5
-
2
2
C．
5
2
D．
5
+
2
2
組卷：343引用：4難度：0.5
解析
6．在四棱錐P-ABCD中，PA⊥平面ABCD，四邊形ABCD是矩形，且AB=3，AD=4，PA=
4
3
5
，則二面角P-BD-A的大小為（　　）
A．30° B．45° C．60° D．75°
組卷：161引用：8難度：0.4
解析
7．已知正項數列{a_n}中，
a
1
=
2
，
a
n
+
1
=
2
a
n
+
3
×
5
n
，則數列{a_n}的通項a_n=（　　）
A．-3×2^n-1 B．3×2^n-1 C．5ⁿ+3×2^n-1 D．5ⁿ-3×2^n-1
組卷：260引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

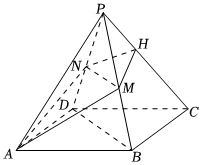21．已知四棱錐P-ABCD，底面ABCD為菱形，PD=PB，H為PC上的點，過AH的平面分別交PB，PD于點M，N，且BD∥平面AMHN．
（1）證明：MN⊥PC；
（2）當H為PC的中點，
PA
=
PC
=
3
AB
，PA與平面ABCD所成的角為60°，求平面PAM與平面AMN所成的銳二面角的余弦值．
組卷：211引用：12難度：0.6
解析
22．已知函數f（x）=lnx-mx²+（1-2m）x+1．
（1）若m=1，求f（x）的極值；
（2）若對任意x＞0，f（x）≤0恒成立，求整數m的最小值．
組卷：631引用：13難度：0.6
解析