人教新版八年級下冊《專題 勾股定理和平行四邊形》2021年同步練習卷（江西省南昌市紅谷灘區鳳凰城上海外國語學校）

一．選擇題（共8小題，滿分24分，每小題3分）

• 1．下列四組數據不能作為直角三角形的三邊長的是（　　）

  A．9，12，15

  B．7，24，25

  C．15，36，39

  D．12，15，20
  組卷：1105引用：6難度：0.7

  解析

• 2．下面幾組數能作為直角三角形三邊長的是（　　）

  A．2，4，5

  B．5，12，13

  C．12，18，22

  D．4，5，8
  組卷：926引用：6難度：0.5

  解析

• 3．已知平行四邊形ABCD中，∠A+∠C=110°，則∠B的度數為（　　）

  A．125°

  B．135°

  C．145°

  D．155°
  組卷：3055引用：22難度：0.5

  解析

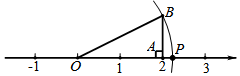• 4．小明學了在數軸上表示無理數的方法后，進行了練習：首先畫數軸，原點為O，在數軸上找到表示數2的點A，然后過點A作AB⊥OA，使AB=1；再以O為圓心，OB的長為半徑作弧，交數軸正半軸于點P，那么點P表示的數是（　　）

  A．2.2

  B． 5

  C． 1 + 2

  D． 6
  組卷：3650引用：20難度：0.3

  解析

• 5．在△ABC中，AB=BC=2，O是線段AB的中點，P是射線CO上的一個動點，∠AOC=60°，則當△PAB為直角三角形時，AP的長為（　　）

  A．1， 3 ，7

  B．1， 5 ， 7

  C．1， 3 ， 7

  D．1，3， 7
  組卷：2062引用：2難度：0.3

  解析

• 6．如圖，在平行四邊形ABCD中，

  AB

  =

  3

  ，AC=2，BD=4，則BC的長是（　　）

  A． 2 3

  B． 7

  C．3

  D．5
  組卷：892引用：9難度：0.7

  解析

• 7．如圖，點O在線段AB上，AO=2，OB=1，OC為射線，且∠BOC=60°，動點P以每秒2個單位長度的速度從點O出發，沿射線OC做勻速運動，設運動時間為t秒．當△ABP是直角三角形時，t的值為（　　）

  A． - 1 + 33 8

  B． 1 + 33 8

  C．1或 - 1 + 33 8

  D．1或 1 + 33 8
  組卷：3937引用：4難度：0.3

  解析

三．解答題（共10小題，滿分80分）

• 21．已知△ABC中，AB=AC．
  （1）如圖1，在△ADE中，若AD=AE，且∠DAE=∠BAC，求證：CD=BE；
  （2）如圖2，在△ADE中，若∠DAE=∠BAC=60°，且CD垂直平分AE，AD=3，CD=4，求BD的長；
  （3）如圖3，在△ADE中，當BD垂直平分AE于H，且∠BAC=2∠ADB時，試探究CD²，BD²，AH²之間的數量關系，并證明．
  
  組卷：21798引用：13難度：0.1

  解析

• 22．如圖，在等邊△ABC中，線段AM為BC邊上的中線，動點D在直線AM上時，以CD為一邊且在CD的下方作等邊△CDE，連接BE．
  （1）填空：∠ACB=

   

  度；
  （2）當點D在線段AM上（點D不運動到點A）時，試求出

  AD

  BE

  的值；
  （3）若AB=8，以點C為圓心，以5為半徑作⊙C與直線BE相交于點P、Q兩點，在點D運動的過程中（點D與點A重合除外），試求PQ的長．
  
  組卷：3670引用：9難度：0.1

  解析