2022年寧夏石嘴山一中高考數學一模試卷（理科）

一、選擇題：本題共12小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|2^x≤

  19

  ，x∈N*}，B={x|log₂（x-1）=0}，則A∩B=（　　）

  A．{1，2}

  B．{2}

  C．?

  D．{0，1，2}
  組卷：26引用：1難度：0.7

  解析

• 2．已知復數

  z

  =

  1

  +

  3

  i

  i

  ，則|z|為（　　）

  A．2

  B．4

  C． 10

  D．10
  組卷：133引用：7難度：0.7

  解析

• 3．設m是直線，α、β是兩個不同的平面，且α⊥β，則“m∥β”是“m⊥α”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：167引用：2難度：0.8

  解析

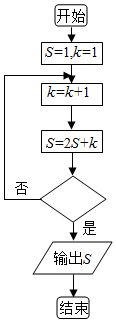• 4．某程序框圖如圖所示，若輸出的S=57，則判斷框內應填（　　）

  A．k＞4？

  B．k＞5？

  C．k＞6？

  D．k＞7？
  組卷：278引用：24難度：0.9

  解析

• 5．《九章算術》是我國古代的數學名著，書中有如下問題：“今有大夫、不更、簪褭、上造、公士五人，共獵得五鹿，欲以爵次分之，問各得幾何？”已知問題中五個爵位是由高到低排列的，古代數學中“以爵次分之”一般表示等差分配，若已知上造得三分鹿之二，即上造分得

  2

  3

  鹿．則以下說法不正確的有（　　）

  A．大夫分得二鹿

  B．不更、上造分得的鹿之和是簪褭的兩倍

  C．不更分得一鹿加三分鹿之一

  D．不更、上造分得的鹿之和與大夫、公士分得的鹿之和相等
  組卷：75引用：5難度：0.8

  解析

• 6．如圖，在三棱錐S-ABC中，點E，F分別是SA，BC的中點，點G在棱EF上，且滿足

  EG

  GF

  =

  1

  2

  ，若

  SA

  =

  a

  ，

  SB

  =

  b

  ，

  SC

  =

  c

  ，則

  SG

  =（　　）

  A． 1 3 a - 1 2 b + 1 6 c	B． 1 3 a + 1 6 b + 1 6 c
  C． 1 6 a - 1 3 b + 1 2 c	D． 1 3 a - 1 6 b + 1 2 c
  組卷：1828引用：20難度：0.9

  解析

• 7．第十三屆冬殘奧會于2022年3月4日至3月13日在北京舉行．現從4名男生，2名女生中選3人分別擔任冬季兩項、單板滑雪、輪椅冰壺志愿者，且至多有1名女生被選中，則不同的選擇方案共有（　　）

  A．72種

  B．84種

  C．96種

  D．124種
  組卷：717引用：11難度：0.7

  解析

四、解答題：本題共5小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．設a＞0，函數f（x）=lnx-ax,g（x）=lnx-

  2

  （

  x

  -

  1

  ）

  x

  +

  1

  ．
  （1）證明：當x＞1時，g（x）＞0恒成立；
  （2）若函數f（x）無零點，求實數a的取值范圍；
  （3）若函數f（x）有兩個相異零點x₁、x₂，求證：x₁x₂＞e²．
  組卷：144引用：3難度：0.1

  解析

[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系xOy中，曲線C的參數方程為

  x = 2 cosθ

  y = 2 sinθ + 2

  （θ為參數），以坐標原點為極點，x軸非負半軸為極軸建立極坐標系．
  （1）求C的極坐標方程；
  （2）若直線l₁，l₂的極坐標方程分別為

  θ

  =

  π

  6

  （

  ρ

  ∈

  R

  ）

  ，

  θ

  =

  2

  π

  3

  （

  ρ

  ∈

  R

  ）

  ，設直線l₁與曲線C的交點為O，M，直線l₂與曲線C的交點為O，N，求△OMN的面積．
  組卷：200引用：11難度：0.3

  解析