2022-2023學年福建省三明市高一（下）期末數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知i為虛數單位，若z?（1+i）=2i,則|z|=（　　）

  A．2

  B． 2

  C．1

  D． 2 2
  組卷：81引用：8難度：0.9

  解析

• 2．已知圓錐底面半徑為1，高為2，則該圓錐側面積為（　　）

  A．2π

  B． 5 π

  C．4π

  D． 2 5 π
  組卷：90引用：4難度：0.7

  解析

• 3．已知平面向量

  a

  ，

  b

  滿足|

  a

  |=|

  b

  |=1，

  a

  ⊥（

  a

  -

  2

  b

  ），則

  a

  與

  b

  的夾角為（　　）

  A． 5 π 6

  B． π 6

  C． 2 π 3

  D． π 3
  組卷：80引用：2難度：0.7

  解析

• 4．一次投籃練習后體育老師統計了第一小組10個同學的命中次數作為樣本，計算出他們的平均命中次數為6，方差為3，后來這個小組又增加了一個同學，投籃命中次數為6，那么這個小組11個同學投籃命中次數組成的新樣本的方差是（　　）

  A．3

  B． 30 11

  C． 20 11

  D． 11 10
  組卷：83引用：2難度：0.8

  解析

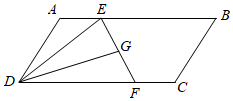• 5．如圖，在平行四邊形ABCD中，

  AE

  =

  1

  3

  AB

  ，

  CF

  =

  1

  3

  CD

  ，

  G

  為EF的中點，則

  DG

  =（　　）

  A． 1 2 AB - 1 2 AD

  B． 1 2 AD - 1 2 AB

  C． 1 3 AB - 1 3 AD

  D． 1 3 AD - 1 3 AB
  組卷：1200引用：7難度：0.5

  解析

• 6．設α，β是兩個不同的平面，l,m是兩條不同的直線，則下列命題中正確的是（　　）

  A．若l⊥α，l⊥β，α∥β

  B．若α⊥β，l?α，m?β，則l⊥m

  C．若m⊥β，α⊥β，則m∥α

  D．若α∥β，且l與α所成的角和m與β所成的角相等，則l∥m
  組卷：82引用：3難度：0.7

  解析

• 7．麒麟山位于三明市區中部，海拔262米，原名牛壟山．在地名普查時，發現山腰有一塊“孔子戲麒麟”石碑，故更現名．山頂的麒麟閣仿古塔造型是八角重檐閣．小李為測量麒麟閣的高度選取了與底部水平的直線AC，如圖，測得∠DAC=30°，∠DBC=45°，AB=18米，則麒麟閣的高度CD約為（參考數據：

  2

  ≈

  1

  .

  414

  ，

  3

  =

  1

  .

  732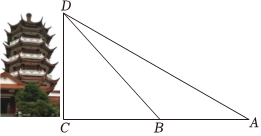

  ）（　　）
  

  A．20.6米

  B．22.6米

  C．24.6米

  D．26.6米
  組卷：45引用：2難度：0.6

  解析

四、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．

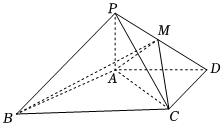• 21．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2，BC=4，PA=

  2

  ．
  （1）求證：AB⊥PC；
  （2）在線段PD上是否存在一點M，使得BM與平面ABCD所成角的正切值為

  26

  26

  ，若存在，求二面角M-AC-D的大小，若不存在，請說明理由．
  組卷：92引用：1難度：0.5

  解析

• 22．已知△ABC的內角A，B，C的對邊分別為a,b,c.點D在BC上，且

  AD

  =

  2

  ．
  （1）若sin∠ADC=2sinB，求c；
  （2）若AD是∠BAC的角平分線，且

  ∠

  BAC

  =

  2

  π

  3

  ，求△ABC周長的最小值．
  組卷：89引用：2難度：0.6

  解析