當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年江蘇省南京外國語學(xué)校高二（上）期末數(shù)學(xué)試卷

發(fā)布：2024/4/20 14:35:0

一．選擇題（共8小題，每題3分，共24分）

1．已知等差數(shù)列{a_n}中，a₃+a₈=22，a₆=7，則a₅的值為（　　）
A．10 B．15 C．20 D．40
組卷：106引用：3難度：0.7
解析
2．函數(shù)f（x）=e^x+ax在x=0處的切線與直線2x-y-5=0平行，則實(shí)數(shù)a=（　　）
A．-1 B．1 C．
1
2
D．
1
4
組卷：336引用：4難度：0.8
解析
3．已知圓C的圓心在x軸上，且經(jīng)過A（5，2），B（-1，4）兩點(diǎn)，則圓C的方程是（　　）
A．（x+2）²+y²=17 B．（x-2）²+y²=13
C．（x-1）²+y²=20 D．（x+1）²+y²=40
組卷：304引用：6難度：0.9
解析
4．下列求導(dǎo)結(jié)果正確的是（　　）
A．[（1-2x）²]′=2-4x B．（cos
π
5
）′=-sin
π
5
C．
[
ln
（
3
x
）
]
′
=
1
3
x
D．（x?cosx）'=cosx-xsinx
組卷：614引用：4難度：0.8
解析
5．設(shè)正項等比數(shù)列{a_n}的前n項和為S_n，且
a
n
+
1
a
n
＜1，若a₃+a₅=20，a₃a₅=64，則S₄=（　　）
A．63或126 B．252 C．120 D．63
組卷：197引用：8難度：0.9
解析
6．設(shè)函數(shù)
f
（
x
）
=
|
x
|
-
1
，
x
∈
[
-
1
，
+
∞
）
2
f
（
x
+
2
）
，
x
∈
（
-
∞
，-
1
）
，若對任意的x∈[m,+∞），都有f（x）≥-4，則m的最小值是（　　）
A．-4 B．-6 C．
-
13
2
D．
-
11
2
組卷：333引用：3難度：0.5
解析
7．已知直線L：
y
=
1
2
x
+
m
與曲線
C
：
y
=
1
2
|
4
-
x
2
|
僅有三個交點(diǎn)，則實(shí)數(shù)m的取值范圍是（　　）
A．
（
-
2
，
2
）
B．
（
-
2
，
2
）
C．
（
1
，
2
）
D．
（
1
，
3
）
組卷：103引用：6難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四．解答題（共5小題，共48分）

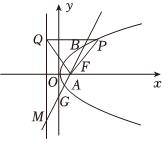20．如圖，已知拋物線y²=2px（p＞0），焦點(diǎn)為F，準(zhǔn)線為直線l,P為拋物線上的一點(diǎn)，過點(diǎn)P作l的垂線，垂足為點(diǎn)Q．當(dāng)P的橫坐標(biāo)為3時，△PQF為等邊三角形．
（1）求拋物線的方程；
（2）過點(diǎn)F的直線交拋物線于A，B兩點(diǎn)，交直線l于點(diǎn)M，交y軸于G．
①若
MA
=
λ
1
AF
，
MB
=
λ
2
BF
，求證：λ₁+λ₂為常數(shù)；
②求
GA
?
GB
的取值范圍．
組卷：302引用：3難度：0.1
解析
21．已知函數(shù)f（x）=xlnx,g（x）=ax²-x（a∈R）．
（1）求f（x）的單調(diào)區(qū)間和極值點(diǎn)；
（2）求使f（x）≤g（x）恒成立的實(shí)數(shù)a的取值范圍；
（3）當(dāng)
a
=
1
8
時，是否存在實(shí)數(shù)m,使得方程
3
f
（
x
）
4
x
+
m
+
g
（
x
）
=
0
有三個不等實(shí)根？若存在，求出m的取值范圍；若不存在，請說明理由．
組卷：165引用：7難度：0.3
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費(fèi)下載

A．（x+2）²+y²=17	B．（x-2）²+y²=13
C．（x-1）²+y²=20	D．（x+1）²+y²=40

A．[（1-2x）²]′=2-4x	B．（cos π 5 ）′=-sin π 5
C． [ ln （ 3 x ） ] ′ = 1 3 x	D．（x?cosx）'=cosx-xsinx

2022-2023學(xué)年江蘇省南京外國語學(xué)校高二（上）期末數(shù)學(xué)試卷

一．選擇題（共8小題，每題3分，共24分）

1．已知等差數(shù)列{an}中，a3+a8=22，a6=7，則a5的值為（ ）

2．函數(shù)f（x）=ex+ax在x=0處的切線與直線2x-y-5=0平行，則實(shí)數(shù)a=（ ）

3．已知圓C的圓心在x軸上，且經(jīng)過A（5，2），B（-1，4）兩點(diǎn)，則圓C的方程是（ ）

4．下列求導(dǎo)結(jié)果正確的是（ ）

5．設(shè)正項等比數(shù)列{an}的前n項和為Sn，且an+1an＜1，若a3+a5=20，a3a5=64，則S4=（ ）

6．設(shè)函數(shù)f（x）=|x|-1，x∈[-1，+∞）2f（x+2），x∈（-∞，-1），若對任意的x∈[m,+∞），都有f（x）≥-4，則m的最小值是（ ）

7．已知直線L：y=12x+m與曲線C：y=12|4-x2|僅有三個交點(diǎn)，則實(shí)數(shù)m的取值范圍是（ ）

四．解答題（共5小題，共48分）

1．已知等差數(shù)列{a_n}中，a₃+a₈=22，a₆=7，則a₅的值為（　　）

2．函數(shù)f（x）=e^x+ax在x=0處的切線與直線2x-y-5=0平行，則實(shí)數(shù)a=（　　）

3．已知圓C的圓心在x軸上，且經(jīng)過A（5，2），B（-1，4）兩點(diǎn)，則圓C的方程是（　　）

4．下列求導(dǎo)結(jié)果正確的是（　　）

5．設(shè)正項等比數(shù)列{a_n}的前n項和為S_n，且
a
n
+
1
a
n
＜1，若a₃+a₅=20，a₃a₅=64，則S₄=（　　）

6．設(shè)函數(shù)
f
（
x
）
=
|
x
|
-
1
，
x
∈
[
-
1
，
+
∞
）
2
f
（
x
+
2
）
，
x
∈
（
-
∞
，-
1
）
，若對任意的x∈[m,+∞），都有f（x）≥-4，則m的最小值是（　　）

7．已知直線L：
y
=
1
2
x
+
m
與曲線
C
：
y
=
1
2
|
4
-
x
2
|
僅有三個交點(diǎn)，則實(shí)數(shù)m的取值范圍是（　　）