2022-2023學年湖北省鄂東南教學改革聯盟學校高二（上）期中數學試卷

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．已知復數z滿足|z-1-i|=1，則|z+1+i|的最大值是（　　）

  A． 2 2 - 1

  B． 2 2 + 1

  C．2

  D． 2 2
  組卷：74引用：2難度：0.8

  解析

• 2．下列說法正確的是（　　）

  A．零向量沒有方向

  B．若 a ? b = a ? c ， （ a ≠ 0 ） ，則 b = c

  C．長度相等的向量叫做相等向量

  D．兩個有共同起點而且相等的向量，其終點必相同
  組卷：488引用：1難度：0.8

  解析

• 3．高二某班參加了“中國神舟十三號載人飛船航空知識答題”競賽，10位評委的打分如下：5，6，6，7，7，8，9，9，10，10，則（　　）

  A．該組數據第60百分位數為8

  B．該組數據第60百分位數為8.5

  C．該組數據中位數為7和8

  D．該組數據中位數為8
  組卷：228引用：2難度：0.7

  解析

• 4．若直線l：cos

  θ

  2

  x

  -

  sin

  θ

  2

  y+1=0，（0≤θ＜π），則直線l的傾斜角為（　　）

  A． θ 2

  B．θ

  C． 3 π 2 - θ 2

  D． π 2 - θ 2
  組卷：49引用：2難度：0.7

  解析

• 5．在空間四邊形OABC中，E、F分別是OA、BC的中點，P為線段EF上一點，且PF=2EP，設

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，則下列等式不成立的是（　　）

  A． OF = 1 2 b + 1 2 c	B． EP = - 1 6 a + 1 6 b + 1 6 c
  C． FP = - 1 3 a + 1 3 b + 1 3 c	D． OP = 1 3 a + 1 6 b + 1 6 c
  組卷：70引用：2難度：0.7

  解析

• 6．若直線kx+y+2-2k=0與曲線

  4

  -

  （

  y

  -

  1

  ）

  2

  +1=x有兩個不同的交點，則實數k的取值范圍是（　　）

  A． （ - ∞ ，- 1 - 2 6 3 ） ∪ [ 5 ， + ∞ ）	B． （ 4 3 ， 4 ]
  C． [ - 2 ，- 1 + 2 6 3 ） ∪ （ 4 3 ， 2 ]	D． （ 4 3 ， + ∞ ）
  組卷：359引用：7難度：0.6

  解析

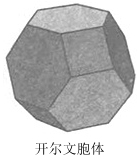• 7．2008年北京奧運會游泳中心（水立方）的設計來于威爾，弗蘭泡沫是對開爾文胞體的改進，如圖，開爾文胞體是一種多面體，它由正六邊形和正方形圍成（其中每一個頂點處有一個正方形和兩個正六邊形），已知該多面體共有24個頂點，且該多面體表面積是

  6

  +

  12

  3

  ，則該多面體的棱長是（　　）

  A．1

  B．2

  C． 3

  D． 3 2
  組卷：91引用：1難度：0.4

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

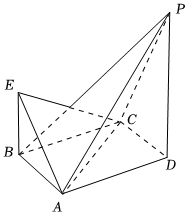• 21．如圖，四棱錐P-ABCD的底面ABCD為菱形，且菱形ABCD的面積為4，PD，BE都與平面ABCD垂直，BE=1，PD=2．
  （1）求三棱錐E-ABC與四棱錐P-ABCD公共部分的體積大小；
  （2）若二面角D-AP-B大小為

  π

  2

  ，求DE與平面PAD所成角的正弦值．
  組卷：39引用：1難度：0.5

  解析

• 22．在△ABC中，已知A（-1，0），B（-2，0），且

  2

  sinB=sinA．
  （1）求頂點C的軌跡E的方程；
  （2）曲線E與y軸交于P，Q兩點，T是直線y=2

  2

  上一點，連TP，TQ分別與E交于M，N兩點（異于P，Q兩點），試探究直線MN是否過定點，若是求定點，若不是說明理由．
  組卷：128引用：3難度：0.4

  解析