2021-2022學年黑龍江省齊齊哈爾市甘南縣高一（下）期末數學試卷

一.單選題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．復數z=

  2

  1

  +

  i

  的虛部為（　　）

  A．1

  B．-1

  C．i

  D．-i
  組卷：11引用：5難度：0.9

  解析

• 2．若a、b∈R，則“a＞b”是“

  （

  a

  +

  1

  ）

  1

  2

  ＞

  （

  b

  +

  1

  ）

  1

  2

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：22引用：3難度：0.8

  解析

• 3．為了了解某道口堵車情況，在今后的三天中，假設每一天堵車的概率均為40%．現采用模擬試驗的方法估計這三天中恰有兩天堵車的概率：先利用計算器產生0到9之間的隨機整數，用1，2，3，4表示堵車，用5，6，7，8，9，0表示不堵車；再以每三個數作為一組，代表這三天的堵車情況．經試驗產生了如下20組隨機數：
  807 066 123 923 471 532 712 269 507 752 443 277 303 927 756 368 840 413 730 086
  據此估計，這三天中恰有兩天堵車的概率近似為（　　）

  A．0.25

  B．0.3

  C．0.35

  D．0.40
  組卷：100引用：6難度：0.7

  解析

• 4．已知m,n是兩條不同的直線，α，β是兩個不同的平面，則以下命題正確的是（　　）

  A．若m∥n,m∥α，n∥β，則α∥β	B．若m⊥n,m⊥α，則n∥α
  C．若m∥α，m⊥n,則n⊥α	D．若m⊥α，m∥β，則α⊥β
  組卷：48引用：4難度：0.7

  解析

• 5．北京時間2021年10月16日0時23分，搭載神舟十三號載人飛船的長征二號F遙十三運載火箭，在酒泉衛星發射中心按照預定時間精準點火發射，約582秒后，神舟十三號載人飛船與火箭成功分離，進入預定軌道，順利將翟志剛、王亞平、葉光富3名航天員送入太空，飛行乘組狀態良好，發射取得圓滿成功．此次航天飛行任務中，火箭起到了非常重要的作用．在不考慮空氣動力和地球引力的理想情況下，火箭在發動機工作期間獲得速度增量v（單位：千米/秒）可以用齊奧爾科夫斯基公式

  v

  =

  ωln

  （

  1

  +

  m

  M

  ）

  來表示，其中，ω（單位：千米/秒）表示它的發動機的噴射速度，m（單位：噸）表示它裝載的燃料質量，M（單位：噸）表示它自身（除燃料外）質量．若某型號的火箭發動機的噴射速度為5千米/秒，要使得該火箭獲得的最大速度v達到第一宇宙速度（7.9千米/秒），則火箭的燃料質量m與火箭自身質量M之比

  m

  M

  約為（　　）

  A．e0.58-1

  B．e1.58

  C．e1.58-1

  D．e0.58
  組卷：69引用：2難度：0.8

  解析

• 6．若a=cos2，b=log₃2，c=log₆4，則（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．c＞b＞a

  D．b＞c＞a
  組卷：22引用：2難度：0.7

  解析

• 7．如圖為2022年北京冬奧會首鋼滑雪大跳臺示意圖，為測量大跳臺最高點P距地面的距離，小明同學在場館內的A點測得P的仰角為30°，∠ABO=120°，∠BAO=30°，AB=60（單位：m），（點A，B，O在同一水平地面上），則大跳臺最高高度OP=（　　）

  A．45m

  B． 45 2 m

  C．60m

  D． 60 3 m
  組卷：114引用：7難度：0.7

  解析

四.解答題：共70分，解答應寫出文字說明、解答過程或演算步驟.

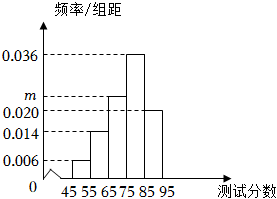• 21．某學校為了了解高二年級學生數學運算能力，對高二年級的200名學生進行了一次測試．已知參加此次測試的學生的分數x_i（i=1，2，…，200）全部介于45分到95分之間，該校將所有分數分成5組：[45，55），[55，65），…，[85，95]，整理得到如下頻率分布直方圖（同組數據以這組數據的中間值作為代表）．
  （1）求m的值，并估計此次校內測試分數的平均值

  x

  ；
  （2）學校要求按照分數從高到低選拔前20名的學生進行培訓，試估計這20名學生的最低分數；
  （3）試估計這200名學生的分數x_i（i=1，2，…，200）的方差s²，并判斷此次得分為52分和94分的兩名同學的成績是否進入到了

  [

  x

  -

  2

  s

  ,

  x

  +

  2

  s

  ]

  范圍內？
  （參考公式：

  s

  2

  =

  1

  n

  n

  ∑

  i

  =

  1

  f

  i

  （

  x

  i

  -

  x

  ）

  2

  ，其中f_i為各組頻數；參考數據：

  129

  ≈

  11

  .

  4

  ）
  組卷：91引用：3難度：0.9

  解析

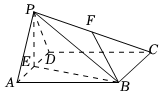• 22．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為2的菱形，∠BAD=60°，△PAD是正三角形，E為線段AD的中點，點F為棱PC上的動點．
  （1）求證：平面PBC⊥平面PBE；
  （2）若平面PAD⊥平面ABCD．
  ①當點F恰為PC中點時，求異面直線PD與BF所成角的余弦值；
  ②在平面PBE內確定一點H，使CH+FH的值最小，并求此時

  BH

  BP

  的值．
  組卷：204引用：5難度：0.5

  解析