2023年陜西省西安市國際港務區鐵一中陸港中學中考數學八模試卷

一、選擇題。(每題3分,共24分)

• 1．-1-2的值為（　　）

  A．-3

  B．1

  C．-1

  D．2
  組卷：349引用：6難度：0.9

  解析

• 2．如圖所示，直線a∥b,∠2=28°，∠1=50°，則∠A=（　　）

  A．32°

  B．78°

  C．22°

  D．20°
  組卷：1466引用：11難度：0.7

  解析

• 3．下列因式分解正確的是（　　）

  A．x2+y2=（x+y）2	B．x2-5x+6=（x-2）（x-3）
  C．-3t2+6t=-3t（t+2）	D．x2y+xy+x=x（xy+y）
  組卷：274引用：3難度：0.9

  解析

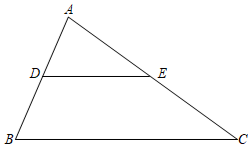• 4．如圖，在△ABC中，點D、E分別是AB、AC的中點，若△ADE的面積是3cm²，則四邊形BDEC的面積為（　　）

  A．12cm2

  B．9cm2

  C．6cm2

  D．3cm2
  組卷：1856引用：22難度：0.7

  解析

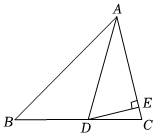• 5．如圖，在△ABC中，∠B=45°，AD是△ABC的角平分線，DE⊥AC，垂足為點E．若DE=2，則BD的長為（　　）

  A．4

  B． 2 3

  C．2

  D． 2 2
  組卷：835引用：5難度：0.7

  解析

• 6．直線

  y

  =

  1

  2

  x

  +

  2

  交x軸于A，交y軸于B，直線AB繞原點旋轉180度后的直線解析式為（　　）

  A． y = 1 2 x - 2

  B． y = 1 2 x + 2

  C． y = - 1 2 x - 2

  D． y = - 1 2 x + 2
  組卷：294引用：2難度：0.5

  解析

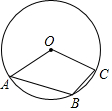• 7．如圖，A，B，C是⊙O上的三點，其中點B是弧AC的三等分點，且弧AB大于弧BC，若∠A=50°，則∠ABC的度數是（　　）

  A．100°

  B．110°

  C．120°

  D．130°
  組卷：367引用：2難度：0.7

  解析

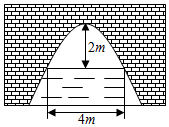• 8．如圖是拋物線型拱橋，當拱頂離水面2m時，水面寬4m.水面上升1.5m,水面寬度為（　　）

  A．1m

  B．2m

  C． 3 m

  D． 2 3 m
  組卷：2547引用：9難度：0.7

  解析

三、解答題。(共81分)

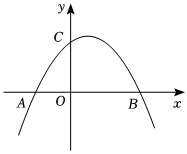• 25．如圖，拋物線y=ax²+bx+c與x軸交于

  A

  （

  -

  2

  ，

  0

  ）

  、

  B

  （

  2

  2

  ，

  0

  ）

  兩點，與y軸交于C（0，2）點．
  （1）求拋物線的解析式；
  （2）證明：△ABC為直角三角形；
  （3）在拋物線上除C點外，是否還存在另外一個點P，使△ABP是直角三角形？若存在，請求出點P的坐標：若不存在，請說明理由．
  組卷：309引用：2難度：0.5

  解析

• 26．問題提出：
  
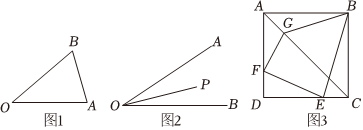
  （1）如圖1，有公共端點的兩條線段OA，OB，且OA=4，OB=5則AB最大值為

  ；最小值為

  ．
  （2）問題探究：如圖2，已知∠AOB=30°，其內部有一點P，OP=6，在∠AOB的兩邊分別有C，D兩點（不同于點O）．使△PCD的周長最小，請畫出草圖，并求出△PCD周長的最小值；
  （3）問題解決：開發商準備對一塊正方形土地進行綠化，要求綠化帶從一個頂點出發到對角線上一點，再到兩邊上一點，最后回到出發點，如圖3，正方形ABCD的邊長為400米，在對角線AC上有一固定點G，且CG=3AG，在AD，DC上取兩點F，E，準備從B到G到F到E再到B修一條綠化帶（綠化帶寬忽略不計），能否設計出最短綠化帶，若能請計算出綠化帶最短長度，若不能說明理由．
  組卷：84引用：2難度：0.5

  解析