當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省佛山市南海區燈湖中學八年級（上）第一次月考數學試卷

發布：2024/12/22 13:0:2

一、選擇題（共10小題，每題3分，共30分）

1．8的算術平方根是（　　）
A．2 B．-2 C．±2
2
D．2
2
組卷：996引用：4難度：0.7
解析
2．下列各式中，是最簡二次根式的是（　　）
A．
1
2
B．
18
C．
5
D．
0
.
4
組卷：1329引用：16難度：0.8
解析
3．滿足下列條件的△ABC不是直角三角形的是（　　）
A．∠A：∠B：∠C=3：4：5 B．BC=1，AC=2，AB=
5
C．BC：AC：AB=3：4：5 D．BC=1，AC=2，AB=
3
組卷：660引用：14難度：0.6
解析
4．下列各點位于平面直角坐標系內第二象限的是（　　）
A．（-3，1） B．（-3，0） C．（3，-1） D．（0，1）
組卷：708引用：13難度：0.7
解析
5．下列運算正確的是（　　）
A．
2
+
3
=
5
B．
8
-
2
=
6
C．
2
?
3
=
5
D．
2
÷
1
2
=2
組卷：447引用：3難度：0.9
解析
6．估算
13
的值（　　）
A．在1到2之間 B．在2到3之間 C．在3到4之間 D．在4到5之間
組卷：548引用：13難度：0.9
解析
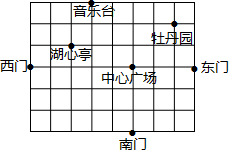7．如圖是人民公園的部分平面示意圖，為準確表示地理位置，可以建立坐標系用坐標表示地理位置，若牡丹園的坐標是（2，2），南門的坐標是（0，-3），則湖心亭的坐標為（　　）
A．（-1，3） B．（-3，1） C．（-3，-1） D．（3，-1）
組卷：1149引用：11難度：0.7
解析
8．已知一個正比例函數的圖象經過點（-2，3），則這個正比例函數的表達式是（　　）
A．y=x+5 B．y=-
3
2
x C．y=-
2
3
x D．y=-2x+3
組卷：415引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（三）（共2小題，每題10分，共20分）

24．在數學課外學習活動中，小明和他的同學遇到一道題：
已知a=
1
2
+
3
，求2a²-8a+1的值．他是這樣解答的：
∵a=
1
2
+
3
=
2
-
3
（
2
+
3
）
（
2
-
3
）
=2-
3
，∴a-2=-
3
，
∴（a-2）²=3，a²-4a+4=3∴a²-4a=-1，
∴2a²-8a+1=2（a²-4a）+1=2×（-1）+1=-1．
請你根據小明的解析過程，解決如下問題：
（1）
1
2
+
1
=
；
（2）化簡
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+
?
+
1
144
+
143
；
（3）若a=
1
26
-
5
，求a⁴-10a³+a²-20a+5的值．
組卷：419引用：5難度：0.7
解析
25．已知：△ABC是等腰直角三角形，動點P在斜邊AB所在的直線上，以PC為直角邊作等腰直角三角形PCQ，其中∠PCQ=90°，探究并解決下列問題：
（1）如圖①，若點P在線段AB上，且AC=2
2
，PA=1，則：
①線段PB=
，PC=
；
②猜想：PA²，PB²，PQ²三者之間的數量關系為
；
（2）如圖②，若點P在AB的延長線上，在（1）中所猜想的結論仍然成立，請你利用圖②給出證明過程；
（3）若動點P滿足
PA
PB
=
1
3
，請直接寫出
PC
AC
的值．
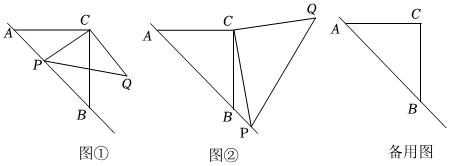組卷：216引用：3難度：0.2
解析