2022年湖南省郴州市高考數學模擬試卷

一、單項選擇題（本題共8小題，每小題只有一個正確選項）

• 1．若集合

  S

  =

  {

  x

  |

  x

  2

  -

  x

  ≥

  1

  ，

  x

  ∈

  R

  }

  ，T={0，1，2，3}，則S∩T=（　　）

  A．{0，1}

  B．{1}

  C．{1，2}

  D．{0，1，2}
  組卷：156引用：3難度：0.8

  解析

• 2．已知復數

  z

  =

  4

  -

  3

  i

  5

  +

  12

  i

  ，則|z|=（　　）

  A． 47 169

  B． 7 17

  C． 25 169

  D． 5 13
  組卷：183引用：3難度：0.9

  解析

• 3．已知圓錐的軸截面是一個正三角形，則其側面積與軸截面面積之比是（　　）

  A． 2 3

  B． 2 3 π 3

  C． 2 π 3

  D． 3 π 2
  組卷：245引用：3難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  3

  sinxcosx

  -

  si

  n

  2

  x

  的圖像的一條對稱軸為（　　）

  A． x = - π 6

  B． x = π 12

  C． x = π 6

  D． x = π 2
  組卷：281引用：2難度：0.7

  解析

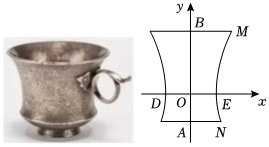• 5．如圖為陜西博物館收藏的國寶——唐金筐寶鈿團花紋金杯，杯身曲線內收，玲瓏嬌美，巧奪天工，是唐代金銀細作的典范之作．該杯的主體部分可以近似看作是離心率為

  5

  的雙曲線

  C

  ：

  x

  2

  -

  y

  2

  b

  2

  =

  1

  （

  b

  ＞

  0

  ）

  的右支與y軸及平行于x軸的兩條直線圍成的曲邊四邊形ABMN繞y軸旋轉一周得到的幾何體，若P為C右支上的一點，F為C的左焦點，則|PF|與P到C的一條漸近線的距離之和的最小值為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：174引用：3難度：0.6

  解析

• 6．△ABC中已知tanA?tanB?tanC=tanA+tanB+tanC且

  A

  +

  B

  =

  3

  π

  4

  ，則（1-tanA）（1-tanB）=（　　）

  A．-2

  B．2

  C．-1

  D．1
  組卷：247引用：5難度：0.7

  解析

• 7．過點（0，b）作曲線y=e^x的切線有且只有兩條，則b的取值范圍為（　　）

  A．（0，1）

  B．（-∞，1）

  C．（-∞，1]

  D．（0，1]
  組卷：190引用：4難度：0.6

  解析

四、解答題：寫出必要的解題步驟或文字說明。（本題共6小題，第17題10分，其余各題每小題10分，共70分）

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右頂點為

  A

  （

  2

  ，

  0

  ）

  ，過左焦點F的直線x=ty-1（t≠0）交橢圓于M，N兩點，交y軸于P點，

  PM

  =λ

  MF

  ，

  PN

  =μ

  NF

  ，記△OMN，△OMF₂，△ONF₂（F₂為C的右焦點）的面積分別為S₁，S₂，S₃．
  （1）證明：λ+μ為定值；
  （2）若S₁=mS₂-μS₃，-4≤λ≤-2，求m的取值范圍．
  組卷：73引用：4難度：0.4

  解析

• 22．已知f（x）=alnx+

  1

  2

  x²-2x（a∈R且a≠0）在（0，+∞）上單調遞增，g（x）=cosx+xsinx.
  （1）當a取最小值時，證明f（x）≤

  1

  2

  x²-x-1恒成立；
  （2）對?x₁∈[-π，π]，?x₂∈[

  1

  e

  ，e]，使得

  f

  （

  x

  2

  ）

  x

  2

  -a≤g（x₁）成立，求實數a的取值范圍．
  組卷：259引用：2難度：0.3

  解析