2023-2024學年浙江省9+1高中聯盟高一（上）期中數學試卷

一、選擇題（本大題共8題，每小題5分，共40分.每小題列出的四個備選項中只有一個是符合題目要求的，不選、多選、錯選均不得分）

• 1．已知集合A={-2，-1，0，1，2}，B={x|x²-x-2≥0}，則A∩（?_RB）=（　　）

  A．{-2，-1，0，1，2}	B．{-1，0，1，2}
  C．{0，1}	D．{-2，-1，2}
  組卷：39引用：1難度：0.7

  解析

• 2．命題“?x＞0，都有x³＞x+1”的否定是（　　）

  A．?x＞0，使得x3≤x+1	B．?x＞0，使得x3＜x+1
  C．?x≤0，都有x3≤x+1	D．?x＞0，都有x3≤x+1
  組卷：52引用：5難度：0.8

  解析

• 3．下列不等式中成立的是（　　）

  A．若a＞b,則an＞bn

  B．若0＜a＜b＜c,則 b a ＜ b + c a + c

  C．若a＞b＞0，則ac2＞bc2

  D．若a＜b＜0，則 1 a ＞ 1 b
  組卷：32引用：2難度：0.8

  解析

• 4．已知某程序研發員開發的小程序在發布時有500名初始用戶，經過t天后，用戶人數m（t）=a?2^kt，其中a和k均為常數．已知小程序發布5天后有2000名用戶，則發布10天后有用戶（　　）名．

  A．10000

  B．8000

  C．400

  D．3500
  組卷：84引用：1難度：0.8

  解析

• 5．冪函數

  f

  （

  x

  ）

  =

  x

  1

  n

  （

  n

  +

  1

  ）

  （

  n

  ∈

  N

  *

  ）

  的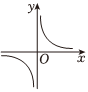大致圖像是（　　）

  A．

  B．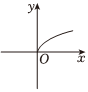

  C．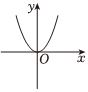

  D．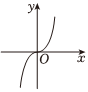
  組卷：188引用：6難度：0.8

  解析

• 6．若奇函數f（x）和偶函數g（x）滿足f（x）+g（x）=3^x+x³+2，則f（1）+g（0）=（　　）

  A． 7 3

  B． 8 3

  C． 19 3

  D． 16 3
  組卷：242引用：5難度：0.8

  解析

• 7．已知函數f（x）=

  a x - 2 ， x ≤ 1

  2 x 2 - x （ x + a ） ， x ＞ 1

  在R上單調遞增，則實數a的取值范圍是（　　）

  A．[1，+∞）

  B．（1，2]

  C． （ 1 ， 3 2 ]

  D． （ 0 ， 3 2 ]
  組卷：96引用：1難度：0.7

  解析

四、解答題（本大題共6題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．已知函數f（x）=

  4

  x

  +

  1

  2

  x

  （x∈R）．
  （1）討論函數f（x）在區間[0，+∞）上的單調性，并用定義法證明；
  （2）若對?x∈[1，2]，都有f（x²-m）＜[f（x）]²-2成立，求實數m的取值范圍．
  組卷：116引用：1難度：0.5

  解析

• 22．已知函數y=f（x）是定義在R上的奇函數，且當x＞0時，f（x）=

  x

  -

  1

  x

  2

  ．
  （1）求函數y=f（x）的解析式；
  （2）若關于x的方程f（x）=m有3個不同的實數根，記為x₁，x₂，x₃（x₁x₂＞0），且

  x

  3

  x

  1

  +

  x

  2

  ≥λ恒成立，求實數λ的取值范圍．
  組卷：151引用：1難度：0.2

  解析