2022-2023學(xué)年湖南省衡陽八中教育集團(tuán)八年級(jí)（下）期末數(shù)學(xué)試卷

一、選擇題（共12小題）

• 1．計(jì)算3^-2的結(jié)果是（　　）

  A．-9

  B．-6

  C．- 1 9

  D． 1 9
  組卷：670引用：49難度：0.9

  解析

• 2．數(shù)據(jù)0.000000017用科學(xué)記數(shù)法表示為（　　）

  A．17×10-8

  B．1.7×10-8

  C．1.7×10-7

  D．1.7×10-9
  組卷：26引用：2難度：0.8

  解析

• 3．已知甲、乙兩組數(shù)據(jù)的平均數(shù)都是3，甲組數(shù)據(jù)的方差

  S

  2

  甲

  =

  1

  5

  ，乙組數(shù)據(jù)的方差

  S

  2

  乙

  =

  2

  5

  ，下列結(jié)論中正確的是（　　）

  A．甲組數(shù)據(jù)比乙組數(shù)據(jù)的波動(dòng)性大

  B．甲組數(shù)據(jù)的比乙組數(shù)據(jù)的波動(dòng)性小

  C．甲、乙兩組數(shù)據(jù)的波動(dòng)性一樣大

  D．甲、乙兩組數(shù)據(jù)的波動(dòng)性無法比較
  組卷：101引用：2難度：0.7

  解析

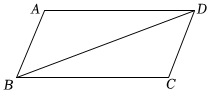• 4．如圖，在四邊形ABCD中，已知AD∥BC．添加下列條件不能判定四邊形ABCD是平行四邊形的是（　　）

  A．AD=BC

  B．AB∥DC

  C．AB=DC

  D．∠A=∠C
  組卷：1607引用：16難度：0.5

  解析

• 5．直線y=2x-2是由y=2x+6（　　）單位長(zhǎng)度得到的．

  A．向右平移8個(gè)	B．向左平移8個(gè)
  C．向下平移8個(gè)	D．向上平移8個(gè)
  組卷：111引用：1難度：0.5

  解析

• 6．如圖，在矩形ABCD中，AE⊥BD，垂足為E，∠DAE：∠BAE=1：3，則∠CAE的度數(shù)（　　）

  A．22.5°

  B．30°

  C．45°

  D．67.5°
  組卷：74引用：1難度：0.7

  解析

• 7．已知點(diǎn)（-2，y₁），（3，y₂），（2，y₃）都在反比例函數(shù)

  y

  =

  6

  x

  的圖象上，那么y₁、y₂、y₃的大小關(guān)系正確的是（　　）

  A．y3＜y1＜y2

  B．y1＜y3＜y2

  C．y1＜y2＜y3

  D．y3＜y2＜y1
  組卷：69引用：1難度：0.5

  解析

• 8．若一次函數(shù)y=（2-m）x+n-4的圖象不經(jīng)過第二象限，則（　　）

  A．m＞2，n＞4

  B．m＜2，n＜4

  C．m＞2，n≥4

  D．m＜2，n≤4
  組卷：230引用：1難度：0.5

  解析

三、解答題（共8小題）

• 25．如圖1，在平面直角坐標(biāo)系中，已知直線CD與x軸交于點(diǎn)C，與直線AB交于點(diǎn)D，其中AC=14，A（8，0），D（2，8）．
  
  （1）求直線CD函數(shù)表達(dá)式；
  （2）如圖2，點(diǎn)P為線段AD上的一點(diǎn)，點(diǎn)Q為直線CD上的一點(diǎn)，連接PC，當(dāng)△PCD的面積為28時(shí)，連接PQ、AQ，求PQ+AQ最小時(shí)，點(diǎn)Q的坐標(biāo)；
  （3）若點(diǎn)E為直線CD上的一點(diǎn)，在平面直角坐標(biāo)系中是否存在點(diǎn)F，使以點(diǎn)A、D、E、F為頂點(diǎn)的四邊形為菱形，若存在，請(qǐng)直接寫出點(diǎn)F的坐標(biāo)：若不存在，請(qǐng)說明理由．
  組卷：128引用：1難度：0.5

  解析

• 26．定義：如果一個(gè)矩形的其中一邊是另一邊的2倍，那么稱這個(gè)矩形為“完美矩形”．如圖1，在矩形ABCD中，AD=2AB，則矩形ABCD是“完美矩形”．E是AD邊上任意一點(diǎn)，連接BE，作BE的垂直平分線分別交AD，BC于點(diǎn)F，G，F(xiàn)G與BE的交點(diǎn)為O，連接BF和EG．
  
  （1）試判斷四邊形BFEG的形狀，并說明理由；
  （2）如圖3，記四邊形BFEG的面積為S₁，“完美矩形”ABCD的面積為S₂，且

  S

  1

  S

  2

  =

  25

  48

  ，若AB=a（a為常數(shù)），且AB＜AD，求FG的長(zhǎng)．（用含有a的代數(shù)式表示）．
  （3）如圖2，在“完美矩形”ABCD中，若AB=3，且AB＜AD，E是邊AD上一個(gè)動(dòng)點(diǎn)，把△ABE沿BE折疊，點(diǎn)A落在點(diǎn)A'處，若A'恰在矩形的對(duì)稱軸上，則AE的長(zhǎng)為

  ．
  組卷：108引用：1難度：0.5

  解析