2021-2022學年江蘇省南京師大蘇州實驗學校高三（上）期中數學試卷

一、單項選擇題本題共8小題，每小題5分，共40分．每小題給出的四個選項中，只有一個選項是正確的．

• 1．已知集合M={x|-2≤x≤3}，N={x|log₂x≤1}，則M∩N=（　　）

  A．[-2，3]

  B．[-2，2]

  C．（0，2]

  D．（0，3]
  組卷：45引用：6難度：0.8

  解析

• 2．若a＞0，b＞0，則“ab＜1”是“a+b＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：69引用：5難度：0.9

  解析

• 3．若tanα=

  3

  4

  ，則

  1

  +

  sin

  2

  α

  1

  -

  2

  si

  n

  2

  α

  =（　　）

  A．- 1 7

  B．-7

  C． 1 7

  D．7
  組卷：43引用：1難度：0.7

  解析

• 4．函數f（x）=（3x-x³）sinx的部分圖象大致為（　　）

  A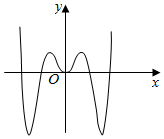．	B．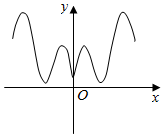
  C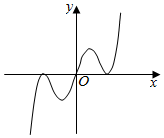．	D．
  組卷：88引用：7難度：0.7

  解析

• 5．已知△ABC是邊長為1的等邊三角形，點D、E分別是邊AB、BC的中點，連接DE并延長到點F，使得DE=2EF，則

  AF

  ?

  BC

  的值為（　　）

  A．- 5 8

  B． 1 4

  C． 1 8

  D． 11 8
  組卷：10543引用：60難度：0.7

  解析

• 6．定義方程f（x）=f'（x）的實數根x.叫做函數f（x）的“躺平點”．若函數g（x）=lnx,h（x）=x³-1的“躺平點”分別為α，β，則α，β的大小關系為（　　）

  A．α≥β

  B．a＞β

  C．α≤β

  D．α＜β
  組卷：95引用：5難度：0.6

  解析

• 7．已知函數f（x）=Asin（ωx-

  π

  6

  ）（A＞0，ω＞0），直線y=1與f（x）的圖象在y軸右側交點的橫坐標依次為a₁，a₂，…，a_k，a_k+1，…，（其中k∈N*），若

  a

  2

  k

  +

  1

  -

  a

  2

  k

  a

  2

  k

  -

  a

  2

  k

  -

  1

  =

  2

  ，則A=（　　）

  A． 2 3 3

  B．2

  C． 2

  D．2 3
  組卷：130引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答時應寫出文字說明、證明過程或演算步驟．

• 21．已知函數f（x）=ax-

  1

  x

  -alnx（a＞0）．
  （1）求f（x）的單調區間；
  （2）若f（x）有兩個極值點x₁，x₂（x₁＜x₂），且不等式

  f

  （

  x

  1

  ）

  +

  f

  （

  x

  2

  ）

  2

  ＞

  f

  （

  x

  1

  +

  x

  2

  2

  ）

  +

  m

  x

  1

  x

  2

  恒成立，求實數m的取值范圍．
  組卷：200引用：3難度：0.5

  解析

• 22．已知函數f（x）=lnx-x+2sinx,f'（x）為f（x）的導函數，求證：
  （1）f'（x）在（0，π）上存在唯一零點；
  （2）f（x）有且僅有兩個不同的零點．
  組卷：163引用：5難度：0.4

  解析