2023-2024學年北京三十五中高二（上）月考數學試卷（10月份）

一、選擇題

• 1．下列說法中正確的是（　　）

  A．任何三個不共線的向量可構成空間向量的一個基底

  B．空間向量的基底有且僅有一個

  C．兩兩垂直的三個非零向量可構成空間的一個基底

  D．基底{ a ， b ， c }中的基向量與基底{ e ， f ， g }中的基向量對應相等
  組卷：201引用：4難度：0.9

  解析

• 2．若直線l的方向向量為

  a

  =（1，-2，3），平面α的法向量為

  n

  =（-3，6，-9），則（　　）

  A．l⊥α	B．l∥α
  C．1?α	D．l與α位置關系不確定
  組卷：92引用：1難度：0.5

  解析

• 3．在正四面體P-ABC中，棱長為2，且E是棱AB中點，則

  PE

  ?

  BC

  的值為（　　）

  A．-1

  B．1

  C． 3

  D． 7 3
  組卷：1157引用：21難度：0.8

  解析

• 4．已知

  PA

  =（2，1，-3），

  PB

  =（-1，2，3），

  PC

  =（7，6，λ），若P，A，B，C四點共面，則λ=（　　）

  A．9

  B．-9

  C．-3

  D．3
  組卷：396引用：7難度：0.8

  解析

• 5．“直線l垂直于平面α內無數條直線”是“直線l垂直于平面α”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：40引用：4難度：0.9

  解析

• 6．在正方體ABCD-A₁B₁C₁D₁中，M，N分別為AD，C₁D₁的中點，O為側面BCC₁B₁的中心，則異面直線MN與OD₁所成角的余弦值為（　　）

  A． 1 6

  B． 1 4

  C． - 1 6

  D． - 1 4
  組卷：97引用：6難度：0.6

  解析

三、解答題

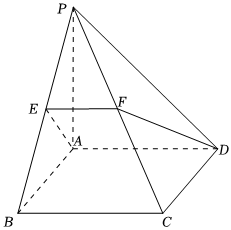• 17．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為2的正方形，側面PAD為等腰直角三角形，且

  ∠

  PAD

  =

  π

  2

  ，點F為棱PC上的點，平面ADF與棱PB交于點E．
  （Ⅰ）求證：EF∥AD；
  （Ⅱ）從條件①、條件②、條件③這三個條件中選擇兩個作為已知，求平面PCD與平面ADFE所成銳二面角的大小．
  條件①：

  AE

  =

  2

  ；
  條件②：平面PAD⊥平面ABCD；
  條件③：PB⊥FD．
  注：如果選擇的條件不符合要求，第（Ⅱ）問得0分；如果選擇多個符合要求的條件分別解答，按第一個解答計分．
  組卷：682引用：9難度：0.4

  解析

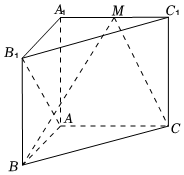• 18．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，AB⊥AC，AB=AC=AA₁=1，M為線段A₁C₁上一點．
  （Ⅰ）求證：BM⊥AB₁；
  （Ⅱ）若直線AB₁與平面BCM所成角為

  π

  4

  ，求點A₁到平面BCM的距離．
  組卷：589引用：6難度：0.6

  解析