2021-2022學年江西省南昌市育山高級中學高一（下）期中數學試卷

一、單選題（本題共12小題，每題5分，共60分）

• 1．已知角α的終邊過點P（4，m）（m≠0），且

  sinα

  =

  m

  5

  ，則cosα的值為（　　）

  A．± 3 5

  B． - 3 5

  C．± 4 5

  D． 4 5
  組卷：601引用：5難度：0.7

  解析

• 2．函數

  y

  =

  cos

  （

  2

  x

  +

  π

  3

  ）

  的圖象（　　）

  A．關于點（ π 3 ，0）對稱	B．關于點（ π 6 ，0）對稱
  C．關于直線 x = π 6 對稱	D．關于直線 x = π 3 對稱
  組卷：611引用：5難度：0.9

  解析

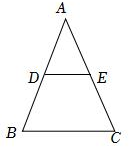• 3．如圖，在△ABC中，AB=AC，D，E分別是AB，AC的中點，則（　　）

  A． AB 與 AC 共線

  B． DE 與 CB 共線

  C． CD 與 AE 相等

  D． AD 與 BD 相等
  組卷：377引用：4難度：0.7

  解析

• 4．已知sinα、cosα是方程5x²-

  5

  x-2=0的兩個實根，且α∈（0，π），則cos（α+

  π

  4

  ）=（　　）

  A． 10 10

  B．- 10 10

  C． 3 10 10

  D．- 3 10 10
  組卷：307引用：4難度：0.7

  解析

• 5．已知扇形OAB的圓心角為4rad,面積為8，則該扇形的周長為（　　）

  A．12

  B．10

  C． 8 2

  D． 4 2
  組卷：230引用：2難度：0.8

  解析

• 6．把函數y=f（x）圖像上所有點的橫坐標縮短到原來的

  1

  2

  倍，縱坐標不變，再把所得曲線向右平移

  π

  3

  個單位長度，得到函數y=sin（x-

  π

  4

  ）的圖像，則f（x）=（　　）

  A．sin（ x 2 - 7 π 12 ）	B．sin（ x 2 + π 12 ）
  C．sin（2x- 7 π 12 ）	D．sin（2x+ π 12 ）
  組卷：8406引用：38難度：0.8

  解析

• 7．已知

  PA

  =

  -

  4

  7

  AB

  ，設

  BP

  =

  λ

  PA

  ，則λ=（　　）

  A． 4 3

  B． - 4 3

  C． - 3 4

  D． 3 4
  組卷：10引用：1難度：0.8

  解析

三、解答題（本題共6題，共70分）

• 21．已知函數f（x）=cos

  x

  4

  sin

  x

  4

  +

  cos

  2

  x

  4

  ．
  （Ⅰ）求函數f（x）的最小正周期和單調遞增區間；
  （Ⅱ）若x∈[0，2π]，求函數f（x）的值域．
  組卷：200引用：2難度：0.6

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  2

  sin

  ωx

  2

  cos

  （

  ωx

  2

  -

  π

  3

  ）

  +

  m

  （

  ω

  ＞

  0

  ）

  ．在下列條件①、條件②、條件③這三個條件中，選擇可以確定ω和m值的兩個條件作為已知．
  （1）求

  f

  （

  π

  4

  ）

  的值；
  （2）若函數f（x）在區間[0，a]上是增函數，求實數a的最大值．
  條件①：f（x）的最小正周期為π；
  條件②：f（x）的最大值與最小值之和為0；
  條件③：f（0）=2．
  組卷：190引用：4難度：0.5

  解析