2023-2024學年吉林省長春二中高三(上)第二次調研數學試卷
發布:2024/9/2 5:0:8
一、選擇題:本題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.已知p:log2x<1,則p的充分不必要條件是( )
A.x<2 B.0<x<2 C.0<x<1 D.0<x<3 組卷:59引用:5難度:0.7 -
2.已知正實數a,b滿足
,則(a+1)(b+9)的最小值是( )1a+9b=6A.36 B.32 C.16 D.8 組卷:131引用:5難度:0.7 -
3.已知函數f(x)=lg[(a2-1)x2+(a+1)x+1]的值域為R,則實數a的取值范圍是( )
A. [1,53]B. (1,53]C. (-∞,-1]∪(53,+∞)D. (-∞,-1)∪[1,53)組卷:421引用:5難度:0.9 -
4.已知函數f(x)=
,對?x1,x2∈R,x1≠x2,滿足(x1-x2)[f(x1)-f(x2)]>0,則實數a的取值范圍是( )ax+1,x≤12x2-(a+1)x+5,x>1A.1<a≤3 B.1<a<3 C.1<a< 52D.1<a≤ 52組卷:84引用:3難度:0.8 -
5.已知定義在R上的函數f(x)滿足f(-x)+f(x)=0,f(x+1)=f(1-x),且當x∈(-1,0)時,f(x)=
(-x),則12-log4=( )f(172)A. 12B.-1 C.- 12D.1 組卷:161引用:3難度:0.8 -
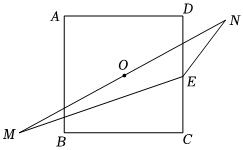 6.如圖,在邊長為2的正方形ABCD中,其對稱中心O平分線段MN,且MN=2BC,點E為DC的中點,則?EM=( )EN
6.如圖,在邊長為2的正方形ABCD中,其對稱中心O平分線段MN,且MN=2BC,點E為DC的中點,則?EM=( )ENA.-3 B.-2 C.- 32D.- 12組卷:145引用:7難度:0.7 -
7.已知函數f(x)=x2+m與函數
g(x)=-ln1x-3x的圖象上至少存在一對關于x軸對稱的點,則實數m的取值范圍是( )(x∈[12,2])A. [54+ln2,2]B. [2-ln2,54+ln2]C. [54+ln2,2+ln2]D.[2-ln2,2] 組卷:239引用:6難度:0.7
四、解答題(本大題共6小題,共70.0分。解答應寫出文字說明,證明過程或演算步驟)
-
21.設函數f(x)=ex+asinx+b.
(1)當a=1,x∈[0,+∞)時,f(x)≥0恒成立,求b的范圍;
(2)若f(x)在x=0處的切線為x-y-1=0,且方程恰有兩解,求實數m的取值范圍.f(x)=m-2xx組卷:199引用:5難度:0.3 -
22.已知函數
,f(x)=sinx+x-1ex.x∈[-π,π2]
(1)求證:f(x)在上單調遞增;[-π,π2]
(2)當x∈[-π,0]時,[f(x)-sinx]ex-cosx≤ksinx恒成立,求k的取值范圍.組卷:59引用:4難度:0.3


