2022-2023學年北京師大二附中高一（下）期中數學試卷

一、選擇題（每題5分）

• 1．sin240°的值為（　　）

  A． - 1 2

  B． 1 2

  C． - 3 2

  D． 3 2
  組卷：350引用：6難度：0.8

  解析

• 2．若復數（2-i）（a+i）的實部與虛部互為相反數，則實數a=（　　）

  A．3

  B． 1 3

  C． - 1 3

  D．-3
  組卷：187引用：6難度：0.8

  解析

• 3．已知向量

  a

  ，

  b

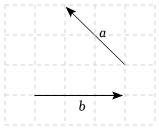  在正方形網格中的位置如圖所示．若網格中每個小正方形的邊長均為1，則

  a

  ?

  b

  =（　　）

  A．6

  B．-6

  C．6 2

  D．-6 2
  組卷：80引用：2難度：0.7

  解析

• 4．半徑為2，弧長為

  π

  5

  的扇形的面積為（　　）

  A． π 5

  B． 2 π 5

  C． π 2 5

  D． 2 π 2 5
  組卷：166引用：3難度：0.9

  解析

• 5．若

  cos

  （

  π

  4

  -

  α

  ）

  =

  4

  5

  ，則

  sin

  （

  π

  4

  +

  α

  ）

  =（　　）

  A． 4 5

  B． 3 5

  C． - 3 5

  D． - 4 5
  組卷：82引用：2難度：0.9

  解析

• 6．已知△ABC中，內角A，B，C所對邊長分別為a,b,c,若

  A

  =

  π

  3

  ，

  b

  =

  2

  acos

  B

  ，

  c

  =

  1

  ，則△ABC的面積等于（　　）

  A． 3 2

  B． 3 4

  C． 3 6

  D． 3 8
  組卷：189引用：14難度：0.7

  解析

• 7．下列函數中，最小正周期為π的奇函數是（　　）

  A．y=sin （ x + π 4 ）	B．y=sin|2x|
  C．y=sinxcosx	D．y=cos2x-sin2x
  組卷：194引用：5難度：0.7

  解析

三、解答題（17題12分，18-19每題15分，20-21每題14分）

• 20．在△ABC中，∠B≠

  π

  2

  ，cos2B=

  3

  cosB-1．
  條件①：sinA=

  3

  sinC、b=2；
  條件②：AC=

  6

  ，BC邊上的高為2；
  條件③：2b=3a、bsinA=1．
  （1）求∠B；
  （2）從條件①、條件②、條件③中選擇一個作為已知，使得△ABC存在且唯一確定時，求△ABC的面積．
  組卷：130引用：1難度：0.5

  解析

• 21．

  a

  =

  （

  3

  sinωx

  ,

  sinωx

  +

  cosωx

  ）

  ，

  b

  =

  （

  2

  cosωx

  ,

  sinωx

  -

  cosωx

  ）

  ，

  f

  （

  x

  ）

  =

  a

  ?

  b

  ，ω＞0．
  （1）若ω=1，求

  f

  （

  π

  6

  ）

  的值；
  （2）若函數f（x）的最小正周期為π．
  ①求ω的值；
  ②當

  x

  ∈

  [

  5

  π

  24

  ，

  5

  π

  12

  ]

  時，對任意t∈R，不等式mt²+mt+3≥f（x）恒成立，求m的取值范圍．
  組卷：33引用：1難度：0.5

  解析