2021-2022學年福建省南平市建甌市芝華中學高二(上)期中數學試卷
發布:2024/9/27 9:0:1
一、單項選擇題:(本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.)
-
1.若平面α⊥β,且平面α的一個法向量為
=(-2,1,?n),則平面β的法向量可以是( )12A.(1,? )12,14B.(2,-1,0) C.(1,2,0) D.(? ,1,2)12組卷:539引用:3難度:0.8 -
2.已知雙曲線
-x2m=1(m>0)的離心率為y2m+6,則其標準方程為( )5A. x22=1-y24B. =1x24-y28C.x2- =1y28D. -x22=1y28組卷:52引用:2難度:0.7 -
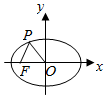 3.如圖,已知橢圓C的中心為原點O,F(-2,0)為C的左焦點,P為C上一點,滿足|OP|=|OF|且|PF|=4,則橢圓C的方程為( )5
3.如圖,已知橢圓C的中心為原點O,F(-2,0)為C的左焦點,P為C上一點,滿足|OP|=|OF|且|PF|=4,則橢圓C的方程為( )5A. +x225=1y25B. +x236=1y216C. +x230=1y210D. +x245=1y225組卷:774引用:17難度:0.9 -
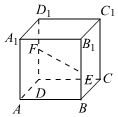 4.如圖,在平行六面體ABCD-A1B1C1D1中,E,F分別在棱BB1和DD1上,且BE=,DF=13BB1.若12DD1,則x+y+z=( )EF=xAB+yAD+zAA1
4.如圖,在平行六面體ABCD-A1B1C1D1中,E,F分別在棱BB1和DD1上,且BE=,DF=13BB1.若12DD1,則x+y+z=( )EF=xAB+yAD+zAA1A.-1 B.0 C. 13D. 16組卷:94引用:3難度:0.8 -
5.兩條平行直線3x+4y-10=0與ax+8y+11=0之間的距離為( )
A. 315B. 3110C. 235D. 2310組卷:573引用:14難度:0.7 -
6.給出下列命題:
①若{,a,b}可以作為空間的一個基底,c與d共線,c≠0,則{d,a,b}也可作為空間的一個基底;d
②已知向量∥a,則b,a與任何向量都不能構成空間的一個基底;b
③A,B,M,N是空間四點,若,BA,BM不能構成空間的一個基底,那么A,B,M,N共面;BN
④已知向量組{,a,b}是空間的一個基底,若c=m+a,則{c,a,b}也是空間的一個基底.m
其中正確命題的個數是( )A.1 B.2 C.3 D.4 組卷:157引用:5難度:0.9 -
7.已知雙曲線C:
-x2a2=1的左、右焦點分別為F1、F2,O為坐標原點.P是雙曲線在第一象限上的點,直線PO,PF2分別交雙曲線C左、右支于另一點M,N.若|PF1|=2|PF2|,且∠MF2N=60°,則雙曲線C的漸近線方程為( )y2b2A.y=± 22xB.y= ±2xC.y=±2x D.y= ±22x組卷:250引用:4難度:0.6
四、解答題:(本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
21.已知F為拋物線y2=x的焦點,點A、B在該拋物線上且位于x軸的兩側,
=2(其中O為坐標原點).OA?OB
(Ⅰ)求證:直線AB恒過定點;
(Ⅱ)直線AB在繞著定點轉動的過程中,求弦AB中點M的軌跡方程.組卷:310引用:4難度:0.5 -
22.已知F1(-2,0),F2(2,0),點P滿足|PF1|-|PF2|=2,記點P的軌跡為E.
(1)求軌跡E的方程;
(2)若直線l過點F2且與軌跡E交于P、Q兩點.
(i)無論直線l繞點F2怎樣轉動,在x軸上總存在定點M(m,0),使MP⊥MQ恒成立,求實數m的值.
(ii)在(i)的條件下,求△MPQ面積的最小值.組卷:1387引用:6難度:0.1


