2022-2023學年山西省運城市教育發展聯盟高二（下）期中數學試卷
發布：2024/8/28 10:0:8
一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一個選項是符合題目要求的.
-
1．某班4名同學去參加校運動會3個場館的志愿者活動，每名同學必須且只能去一個場館，則不同的選擇方法有（ ）
組卷：91引用：3難度：0.8 -
2．在
的展開式中，含x5項的系數為（ ）（x-2x）7組卷：96引用：2難度：0.7 -
3．某校為了研究學生的性別和對待某一活動的態度（支持與不支持）的關系，運用2×2列聯表進行獨立性檢驗．整理所得數據后發現，若依據α=0.010的獨立性檢驗，則認為學生性別與是否支持該活動無關；若依據α=0.025的獨立性檢驗，則認為學生性別與是否支持該活動有關，則K2的值可能為（ ）
P（K2≥k0） 0.100 0.050 0.025 0.010 0.001 k0 2.706 3.841 5.024 6.635 10.828 組卷：151引用：4難度：0.9 -
4．下列說法錯誤的是（ ）
組卷：227引用：5難度：0.8 -
5．已知離散型隨機變量X的分布列服從兩點分布，且P（X=0）=2-5P（X=1）=a,則a=（ ）
組卷：255引用：3難度：0.8 -
6．設某批產品中，甲、乙、丙三個車間生產的產品分別為50%，30%，20%，甲、乙車間生產的產品的次品率分別為3%，5%，現從中任取一件，若取到的是次品的概率為3.6%，則推測丙車間的次品率為（ ）
組卷：380引用：4難度：0.7 -
7．甲、乙兩名高校畢業生準備去北京、上海、廣州、杭州、南京、西安六個城市中選擇一個城市實習，記事件A為“甲和乙至少一人選擇北京”，事件B為“甲和乙選擇的城市不同”，則P（B|A）=（ ）
組卷：166引用：2難度：0.9
四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟
-
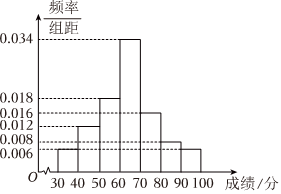21．基礎學科招生改革試點，也稱強基計劃，是教育部開展的招生改革工作，主要是為了選拔培養有志于服務國家重大戰略需求且綜合素質優秀或基礎學科拔尖的學生．強基計劃的校考由試點高校自主命題，校考過程中筆試通過后才能進入面試環節．某省高三2022年有10000名學生報考某試點高校，隨機抽取100名學生的筆試成績，并以此為樣本繪制了樣本頻率分布直方圖，如圖所示．規定筆試成績高于70分的學生進入面試環節．
（1）現從該樣本中隨機抽取兩名學生的筆試成績，求這兩名學生中恰有一名學生進入面試環節的概率；
（2）若該省所有報考某試點高校的學生成績X近似服從正態分布N（μ，σ2），其中σ≈15，μ為樣本平均數的估計值（同一組數據用該組區間的中點值作代表），試估計這10000名報考學生中成績超過94分的學生數（結果四舍五入到整數）．
附參考數據：若隨機變量X服從正態分布N（μ，σ2），則P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973．組卷：102引用：2難度：0.6 -
22．某學校開展投籃比賽活動，比賽規則是：每名選手投籃n次（n≥3，n∈N*），每次投籃，若投進，則下一次站在三分線處投籃；若沒有投進，則下一次站在兩分線處投籃．規定每名選手第一次站在兩分線處投籃．站在兩分線處投進得2分，否則得0分；站在三分線處投進得3分，否則得0分．已知小明站在兩分線處投籃投進的概率為0.6，站在三分線處投籃投進的概率為0.4，且每次投籃相互獨立．
（1）記小明前2次投籃累計得分為X，求X的分布列和數學期望；
（2）記第k次投籃時，小明站在三分線處投籃的概率為ak，k=1，2，?，n,求ak的表達式．組卷：50引用：2難度：0.6