當前位置：試卷中心 > 試卷詳情

2022-2023學年吉林省實驗中學高二（上）期中數學試卷

發布：2024/11/9 21:30:1

一、單選題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知向量
a
=
（
0
，-
1
，
1
）
與
b
=
（
0
，
2
k
-
3
，
k
2
）
共線，則實數k=（　　）
A．0 B．1 C．-1或3 D．-3或1
組卷：52引用：1難度：0.7
解析
2．直線
x
-
3
y
-
1
=
0
的一個方向向量是（　　）
A．
（
1
，
3
）
B．
（
1
，-
3
）
C．
（
1
，
3
3
）
D．
（
1
，-
3
3
）
組卷：65引用：1難度：0.8
解析
3．已知A（-3，4），B（1，a）兩點到直線l：2x+y-1=0的距離相等，則a=（　　）
A．2或-4 B．-2或4 C．2或4 D．-2或-4
組卷：92引用：3難度：0.7
解析
4．點P（3，m）與圓（x+1）²+y²=9的位置關系是（　　）
A．在圓內 B．在圓外 C．在圓上 D．不確定
組卷：84引用：2難度：0.7
解析
5．橢圓
x
2
m
2
+
1
+
y
2
m
2
=
1
（
m
＞
0
）
的焦點為F₁，F₂，上頂點為A，若
∠
F
1
A
F
2
=
π
3
，則橢圓的離心率為（　　）
A．
1
4
B．
3
4
C．
1
2
D．
2
2
組卷：632引用：4難度：0.8
解析
6．在直三棱柱ABC-A₁B₁C₁中，
CA
=
2
2
，CB=2，∠BCA=90°，M是A₁B₁的中點，以C為坐標原點，建立如圖所示的空間直角坐標系，若
A
1
B
⊥
C
B
1
，則異面直線CM與A₁B夾角的余弦值為（　　）
A．
3
7
14
B．
-
2
3
7
C．
-
3
7
14
D．
2
3
7
組卷：35引用：1難度：0.7
解析
7．已知F₁、F₂分別為橢圓
x
2
4
+
y
2
=
1
的左右焦點，點P在橢圓上，且
P
F
1
?
P
F
2
＜
0
，則點P橫坐標的取值范圍是（　　）
A．
（
-
2
，-
4
2
3
）
∪
（
4
2
3
，
2
）
B．
（
-
2
6
3
，
2
6
3
）
C．
（
-
4
2
3
，
4
2
3
）
D．
[
-
2
，-
2
6
3
）
∪
（
2
6
3
，
2
]
組卷：146引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演步驟．

22．已知橢圓C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右頂點分別為A、B，上頂點M與左右頂點連線MA，MB的斜率乘積為-
3
4
，焦距為4．
（1）求橢圓C的方程；
（2）設點P為橢圓上異于A，B的點，直線AP與y軸的交點為Q，過坐標原點O作ON∥AP交橢圓于N點，試探究
|
AP
|
?
|
AQ
|
|
ON
|
2
是否為定值，若是，求出該定值；若不是，請說明理由．
組卷：79引用：4難度：0.5
解析

五、附加題：（自愿作答）本題共1小題，共20分．解答應寫出文字說明、證明過程或演算步驟．

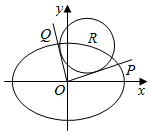23．在平面直角坐標系xOy中，已知R（m,n）是橢圓C：
x
2
18
+
y
2
9
=
1
上一點，從原點O向圓R：（x-m）²+（y-n）²=6作兩條切線，分別交橢圓C于P、Q兩點．
（1）若點R在第一象限，且直線OP⊥OQ，求圓R的方程；
（2）若直線OP、OQ的斜率存在，并分別記為k₁、k₂，求k₁?k₂的值；
（3）試問|OP|²+|OQ|²是否為定值？若是，求出該值；若不是，說明理由．
組卷：68引用：3難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ - 2 ，- 4 2 3 ） ∪ （ 4 2 3 ， 2 ）	B．（ - 2 6 3 ， 2 6 3 ）
C．（ - 4 2 3 ， 4 2 3 ）	D． [ - 2 ，- 2 6 3 ） ∪ （ 2 6 3 ， 2 ]

2022-2023學年吉林省實驗中學高二（上）期中數學試卷

一、單選題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知向量a=（0，-1，1）與b=（0，2k-3，k2）共線，則實數k=（ ）

2．直線x-3y-1=0的一個方向向量是（ ）

3．已知A（-3，4），B（1，a）兩點到直線l：2x+y-1=0的距離相等，則a=（ ）

4．點P（3，m）與圓（x+1）2+y2=9的位置關系是（ ）

5．橢圓x2m2+1+y2m2=1（m＞0）的焦點為F1，F2，上頂點為A，若∠F1AF2=π3，則橢圓的離心率為（ ）

6．在直三棱柱ABC-A1B1C1中，CA=22，CB=2，∠BCA=90°，M是A1B1的中點，以C為坐標原點，建立如圖所示的空間直角坐標系，若A1B⊥CB1，則異面直線CM與A1B夾角的余弦值為（ ）

7．已知F1、F2分別為橢圓x24+y2=1的左右焦點，點P在橢圓上，且PF1?PF2＜0，則點P橫坐標的取值范圍是（ ）

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演步驟．

五、附加題：（自愿作答）本題共1小題，共20分．解答應寫出文字說明、證明過程或演算步驟．

1．已知向量
a
=
（
0
，-
1
，
1
）
與
b
=
（
0
，
2
k
-
3
，
k
2
）
共線，則實數k=（　　）

2．直線
x
-
3
y
-
1
=
0
的一個方向向量是（　　）

3．已知A（-3，4），B（1，a）兩點到直線l：2x+y-1=0的距離相等，則a=（　　）

4．點P（3，m）與圓（x+1）²+y²=9的位置關系是（　　）

5．橢圓
x
2
m
2
+
1
+
y
2
m
2
=
1
（
m
＞
0
）
的焦點為F₁，F₂，上頂點為A，若
∠
F
1
A
F
2
=
π
3
，則橢圓的離心率為（　　）

6．在直三棱柱ABC-A₁B₁C₁中，
CA
=
2
2
，CB=2，∠BCA=90°，M是A₁B₁的中點，以C為坐標原點，建立如圖所示的空間直角坐標系，若
A
1
B
⊥
C
B
1
，則異面直線CM與A₁B夾角的余弦值為（　　）

7．已知F₁、F₂分別為橢圓
x
2
4
+
y
2
=
1
的左右焦點，點P在橢圓上，且
P
F
1
?
P
F
2
＜
0
，則點P橫坐標的取值范圍是（　　）