2010-2011學年江蘇省南通市啟東中學高三（上）數(shù)學寒假作業(yè)（11）

一、填空題：本大題共14小題，每小題5分，滿分70分

• 1．計算復數(shù)

  3

  +

  i

  1

  -

  i

  =

  ．
  組卷：88引用：6難度：0.7

  解析

• 2．若實數(shù)x,y滿足不等式組

  2 x - y ≥ 0

  x + y - 3 ≥ 0

  3 x + y - 8 ≤ 0

  則3x-y的最小值是

  ．
  組卷：3引用：5難度：0.5

  解析

• 3．若等比數(shù)列{a_n}的前n項和S_n滿足：a_n+1=a₁S_n+1（n∈N^*），則a₁=

  ．
  組卷：27引用：6難度：0.7

  解析

• 4．如圖是某個函數(shù)求值的程序框圖，則滿足該程序的函數(shù)解析式為
  

  
  ．
  
  組卷：18引用：7難度：0.5

  解析

• 5．定義在R上的函數(shù)f（x）滿足

  f

  （

  x

  ）

  =

  2 1 - x x ≤ 0

  f （ x - 1 ） - f （ x - 2 ） ， x ＞ 0 .

  則f（-1）=

  ，f（33）=

  ．
  組卷：9引用：3難度：0.7

  解析

• 6．若雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的兩個焦點為F₁，F(xiàn)₂，P為雙曲線上一點，且|PF₁|=3|PF₂|，則該雙曲線離心率的取值范圍是

  ．
  組卷：112引用：11難度：0.7

  解析

• 7．已知a₀≠0．
  ①設方程a₀x+a₁=0的1個根是x₁，則x₁=-

  a

  1

  a

  0

  ；
  ②設方程a₀x²+a₁x+a₂=0的2個根是x₁，x₂，則x₁x₂=

  a

  2

  a

  0

  ；
  ③設方程a₀x³+a₁x²+a₂x+a₃=0的3個根是x₁，x₂，x₃，則x₁x₂x₃=-

  a

  3

  a

  0

  ；
  ④設方程a₀x⁴+a₁x³+a₂x²+a₃x+a₄=0的4個根是x₁，x₂，x₃，x₄，則x₁x₂x₃x₄=

  a

  4

  a

  0

  ；
  …
  由以上結論，推測出一般的結論：
  設方程a₀xⁿ+a₁x^n-1+a₂x^n-2+…+a_n-1x+a_n=0的n個根是x₁，x₂，…，x_n，
  則x₁x₂…x_n=

  ．
  組卷：18引用：2難度：0.7

  解析

• 8．△ABC的三內角A、B、C所對邊的長分別為a、b、c,且（sinA+sinC）（sinA-sinC）=sinB（sinA-sinB），則角C的大小為

  ．
  組卷：23引用：1難度：0.5

  解析

三、加試題部分（每題10分）

• 23．已知：a,b∈R⁺，n＞1，n∈N^*，求證：

  a

  n

  +

  b

  n

  2

  ≥

  （

  a

  +

  b

  2

  ）

  n

  ．
  組卷：93引用：1難度：0.5

  解析

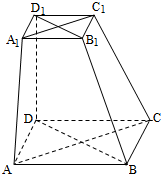• 24．如圖，在六面體ABCD-A₁B₁C₁D₁中，四邊形ABCD是邊長為2的正方形，四邊形A₁B₁C₁D₁是邊長為1的正方形，DD₁⊥平面A₁B₁C₁D₁，DD₁⊥平面ABCD，DD₁=2．
  （Ⅰ）求證：A₁C₁與AC共面，B₁D₁與BD共面；
  （Ⅱ）求證：平面A₁ACC₁⊥平面B₁BDD₁；
  （Ⅲ）求二面角A-BB₁-C的大小（用反三角函數(shù)值表示）．
  組卷：431引用：5難度：0.1

  解析