2022-2023學年江蘇省南京外國語學校高三（上）月考數學試卷

一、選擇題（共5小題）

• 1．已知集合A={x|y=ln（x-1）}，集合

  B

  =

  {

  y

  |

  y

  =

  （

  1

  2

  ）

  x

  ，

  x

  ＞

  -

  2

  }

  ，則A∩B=（　　）

  A．?

  B．[1，4）

  C．（1，4）

  D．（4，+∞）
  組卷：125引用：6難度：0.8

  解析

• 2．已知f（x+1）是偶函數且在[0，+∞）上是單調遞增，且滿足f（2）=0，則不等式f（2x-1）≥0的解集是（　　）

  A．（-∞，0]∪[1，+∞）	B． （ - ∞ ， 1 2 ] ∪ [ 3 2 ， + ∞ ）
  C． [ 3 2 ， + ∞ ）	D． （ - ∞ ，- 3 2 ] ∪ [ 3 2 ， + ∞ ）
  組卷：227引用：5難度：0.7

  解析

• 3．已知實數x,y滿足x＞y＞0，且x+y=1，則

  2

  x

  +

  3

  y

  +

  1

  x

  -

  y

  的最小值為（　　）

  A． 10 3

  B． 3 2 + 2

  C．3+2 2

  D．2 2
  組卷：1386引用：2難度：0.6

  解析

• 4．設f（x）=|x-1|（x+1）-x,若關于x的方程f（x）=k有三個不同的實數解，則實數k的取值范圍是（　　）

  A． 1 ＜ k ＜ 5 4

  B． - 1 ＜ k ＜ 5 4

  C．0＜k＜1

  D．-1＜k＜1
  組卷：130引用：7難度：0.7

  解析

• 5．已知a=4ln3^π，b=3ln4^π，c=4lnπ³，則a,b,c的大小關系是（　　）

  A．c＜b＜a

  B．b＜c＜a

  C．b＜a＜c

  D．a＜b＜c
  組卷：614引用：23難度：0.7

  解析

二.多選題（共6小題）

• 6．設復數z₁，z₂在復平面內的對應點關于虛軸對稱，z₁=2+i,則（　　）

  A．z2=-2-i	B．z2的虛部為1
  C．z1?z2=-5	D．z1?z2=3
  組卷：32引用：2難度：0.8

  解析

• 7．有6個相同的球，分別標有數字1，2，3，4，5，6．從中有放回的隨機取兩次，每次取1個球，甲表示事件“第一次取出的球的數字是1”，乙表示事件“第二次取出的球的數字是2”．丙表示事件“兩次取出的球的數字之和是8”，丁表示事件“兩次取出的球的數字之和是7”，則（　　）

  A．甲與丙相互獨立	B．甲與丁相互獨立
  C．乙與丙不相互獨立	D．丙與丁相互獨立
  組卷：923引用：8難度：0.8

  解析

四.解答題（共7小題）

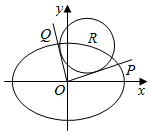• 20．如圖，在平面直角坐標系xOy中，已知R（x₀，y₀）是橢圓C：

  x

  2

  24

  +

  y

  2

  12

  =1上的一點，從原點O向圓R：（x-x₀）²+（y-y₀）²=8作兩條切線，分別交橢圓于點P，Q．
  （1）若R點在第一象限，且直線OP，OQ互相垂直，求圓R的方程；
  （2）若直線OP，OQ的斜率存在，并記為k₁，k₂，求k₁?k₂的值；
  （3）試問OP²+OQ²是否為定值？若是，求出該值；若不是，說明理由．
  組卷：1026引用：17難度：0.1

  解析

• 21．已知函數f（x）=lnx+x-ax²，a∈R．
  （1）若f（x）在x=1處取得極值，求a的值；
  （2）設g（x）=f（x）+（a-3）x,試討論函數g（x）的單調性；
  （3）當a=-2時，若存在正實數x₁，x₂滿足f（x₁）+f（x₂）+3x₁x₂=0，求證：x₁+x₂

  ＞

  1

  2

  ．
  組卷：446引用：5難度：0.1

  解析