2023年天津市濱海新區塘沽一中等十二校聯考高考數學模擬試卷（二）

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x∈Z|x²-x-2≤0}，集合

  B

  =

  {

  x

  |

  y

  =

  1

  -

  log

  2

  x

  }

  ，則A∩B=（　　）

  A．[-1，2]

  B．（1，2]

  C．{1，2}

  D．{-1，1，2}
  組卷：416引用：5難度：0.8

  解析

• 2．設向量

  a

  =

  （

  1

  ，-

  sinθ

  ）

  ，

  b

  =

  （

  sin

  2

  θ

  ，

  sinθ

  ）

  ，則“

  a

  ⊥

  b

  ”是“tanθ=2”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：72引用：3難度：0.7

  解析

• 3．函數

  f

  （

  x

  ）

  =

  0 ， x = 0

  sinx ln | x | ， x ≠ 0

  的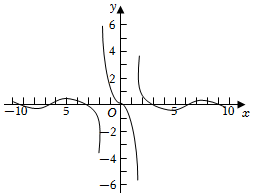大致圖象為（　　）

  A．	B．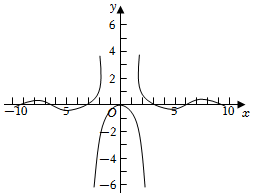
  C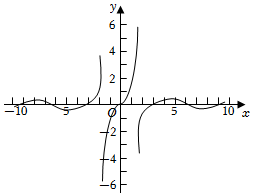．	D．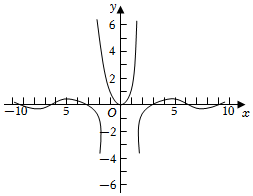
  組卷：184引用：2難度：0.8

  解析

• 4．已知

  5

  a

  =

  2

  2

  ，4^b=n,若

  ab

  =

  3

  2

  ，則n的值為（　　）

  A． 5

  B．5

  C． 5 5

  D．25
  組卷：587引用：1難度：0.7

  解析

• 5．下列說法正確的是（　　）

  A．若a=0.50.6，b=0.60.5，c=log93，則c＞b＞a

  B．若將6名教師分到3所中學任教，每所學校至少一名教師且人數互不相同，則有320種不同的分法

  C．一組數據為148，150，151，153，153，154，155，156，156，158，163，165，則這組數據的上四分位數是156

  D．投擲一枚質地均勻的骰子兩次，記事件A={兩次的點數均為奇數}，事件B={兩次的點數之和為4}，則P（B|A）= 2 9
  組卷：322引用：3難度：0.6

  解析

• 6．已知函數f（x）=sinxcosx+cos²x,x∈R，下列命題中：
  ①f（x）的最小正周期是π，最大值是

  2

  +

  1

  2

  ；
  ②

  f

  （

  x

  ）

  +

  f

  （

  π

  2

  -

  x

  ）

  =

  1

  +

  sin

  2

  x

  ；
  ③f（x）的單調增區間是

  [

  -

  3

  π

  8

  +

  kπ

  ，

  π

  8

  +

  kπ

  ]

  （k∈Z）；
  ④將f（x）的圖象向右平移

  π

  8

  個單位得到的函數是偶函數．
  其中正確個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：464引用：2難度：0.6

  解析

三、解答題：本大題共5小題，共75分.解答應寫出文字說明、證明過程或演算步驟.

• 19．已知橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的兩個焦點與短軸的一個端點是直角三角形的三個頂點，直線l：y=-x+3與橢圓E相切于點T．
  （1）求橢圓E的離心率；
  （2）求橢圓E的標準方程及點T的坐標；
  （3）設O為坐標原點，直線l'平行于直線OT，與橢圓E交于不同的兩點A、B，且與直線l交于點P，那么是否存在常數λ，使得|PT|²=λ|PA|?|PB|？如果存在，求出λ的值；如果不存在，請說明理由．
  組卷：505引用：4難度：0.5

  解析

• 20．設函數f（x）=

  e

  2

  x

  +lnx（x＞0）．
  （Ⅰ）求f（x）的單調區間；
  （Ⅱ）已知a,b∈R，曲線y=f（x）上不同的三點（x₁，f（x₁）），（x₂，f（x₂）），（x₃，f（x₃））處的切線都經過點（a,b）．證明：
  （ⅰ）若a＞e,則0＜b-f（a）＜

  1

  2

  （

  a

  e

  -1）；
  （ⅱ）若0＜a＜e,x₁＜x₂＜x₃，則

  2

  e

  +

  e

  -

  a

  6

  e

  2

  ＜

  1

  x

  1

  +

  1

  x

  3

  ＜

  2

  a

  -

  e

  -

  a

  6

  e

  2

  ．
  （注：e=2.71828…是自然對數的底數）
  組卷：2203引用：6難度：0.1

  解析