2022-2023學年浙江省寧波市慈溪市高三（上）期末數學試卷

一、選擇題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．已知角α的終邊經過點

  （

  -

  1

  ，

  3

  ）

  ，則tanα=（　　）

  A． - 3

  B． 3

  C． - 3 3

  D． 3 3
  組卷：160引用：2難度：0.7

  解析

• 2．已知拋物線y²=2px（p＞0）的焦點與雙曲線

  x

  2

  -

  y

  2

  2

  =

  1

  的其中一個焦點相同，則p=（　　）

  A．1

  B．2

  C． 3

  D． 2 3
  組卷：126引用：1難度：0.8

  解析

• 3．已知集合A={x|y=2x,x∈R}，B={（x,y）|y=x+1，x,y∈R}，則（　　）

  A．A∩B={1，2}

  B．A∩B={（1，2）}

  C．A=B=R

  D．A∩B=?
  組卷：60引用：1難度：0.8

  解析

• 4．若A，B，C，D，E五人排隊照相，則A，B兩人不相鄰的概率為（　　）

  A． 4 5

  B． 3 5

  C． 1 2

  D． 1 5
  組卷：47引用：1難度：0.7

  解析

• 5．若二項式（1+2x）ⁿ（n∈N^*）的展開式中第6項與第7項的系數相等，則此展開式中二項式系數最大的項是（　　）

  A．448x3

  B．1120x4

  C．1792x5

  D．1792x6
  組卷：408引用：2難度：0.8

  解析

• 6．如圖，是某種型號的家用燃氣瓶，其盛氣部分近似可以看作由一個半球和一個圓柱體組成，設球的半徑為R，圓柱體的高為h,若要保持圓柱體的容積為定值V=3π立方米，則為使制造這種燃氣瓶所用材科最省（溫馨提示：即由半球和圓柱體組成的幾何體表面積最小），此時

  R

  h

  =（　　）

  A． 2 2

  B． 1 2

  C． 1 3

  D． 1 4
  組卷：91引用：1難度：0.7

  解析

• 7．在△ABC中，內角A，B，C的對應邊分別為a,b,c,已知bsin（B+C）=asin

  A

  +

  C

  2

  ，且△ABC的面積為2

  3

  ，則△ABC周長的最小值為（　　）

  A． 2 2

  B． 2 3

  C． 6 2

  D． 6 + 2 3
  組卷：401引用：2難度：0.6

  解析

四、解答題（本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟）

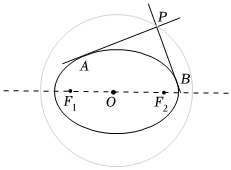• 21．法國數學家加斯帕爾?蒙日被譽為畫法幾何之父．他在研究橢圓切線問題時發現了一個有趣的重要結論：一橢圓的任兩條互相垂直的切線交點的軌跡是一個圓，尊稱為蒙日圓，且蒙日圓的圓心是該橢圓的中心，半徑為該橢圓的長半軸與短半軸平方和的算術平方根．
  已知在橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  中，離心率

  e

  =

  1

  2

  ，左、右焦點分別是F₁、F₂，上頂點為Q，且|QF₂|=2，O為坐標原點．
  （1）求橢圓C的方程，并請直接寫出橢圓C的蒙日圓的方程；
  （2）設P是橢圓C外一動點（不在坐標軸上），過P作橢圓C的兩條切線，過P作x軸的垂線，垂足H，若兩切線斜率都存在且斜率之積為

  -

  1

  2

  ，求△POH面積的最大值．
  組卷：118引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  （

  x

  -

  1

  x

  ）

  -

  klnx

  ,

  k

  ＞

  0

  ．
  （1）當k=3時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若對?x∈（0，1），f（x）＜0恒成立，求k的取值范圍；
  （3）求證：對?x∈（0，1），不等式

  e

  x

  x

  2

  +

  1

  ＜

  x

  2

  -

  1

  xlnx

  恒成立．
  組卷：132引用：1難度：0.3

  解析