2023-2024學年上海市青浦區朱家角中學高二（上）期中數學試卷

一、填空題（4*12=48）

• 1．直線x+y-1=0的傾斜角大小是

  ．
  組卷：42引用：2難度：0.8

  解析

• 2．已知向量

  a

  =（1，2，-2），則向量

  a

  的單位向量

  a

  0

  =

  ．
  組卷：369引用：4難度：0.8

  解析

• 3．以點（1，2）為圓心，與直線4x+3y-35=0相切的圓的方程是

  ．
  組卷：464引用：15難度：0.7

  解析

• 4．直線x+3y-1=0與2x-y+7=0的夾角大小為

  ．
  組卷：70引用：4難度：0.7

  解析

• 5．已知直線l₁：

  3

  x

  -

  2

  y

  +

  2

  =

  0

  ，直線l₂：

  3

  x

  -

  2

  y

  +

  1

  =

  0

  ，則l₁與l₂之間的距離為

  ．
  組卷：40引用：2難度：0.5

  解析

• 6．若向量

  a

  =（4，2，-4），

  b

  =（6，-3，2），則（2

  a

  -3

  b

  ）?（

  a

  +2

  b

  ）=

  ．
  組卷：285引用：13難度：0.7

  解析

• 7．若一個圓柱的側面積是4π，高為1，則這個圓柱的體積是

  ．
  組卷：169引用：5難度：0.8

  解析

三、簡答題（8+10+12+12+14=56）

• 20．已知正三棱柱ABC-A₁B₁C₁中，AA₁=2AC=2，延長CB至D，使CB=BD．
  （1）求證：CA⊥DA₁；
  （2）求二面角B₁-AD-C的大小（結果用反三角函數值表示）．
  組卷：183引用：4難度：0.6

  解析

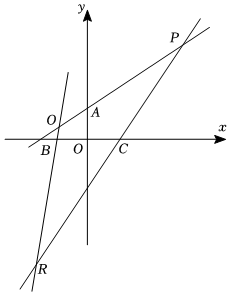• 21．已知點P和非零實數λ，若兩條不同的直線l₁，l₂均過點P，且斜率之積為λ，則稱直線l₁，l₂是一組“P_λ共軛線對”，如直l₁：y=2x,l₂：

  y

  =

  -

  1

  2

  x

  是一組“O_-1共軛線對”，其中O是坐標原點．
  （1）已知點A（0，1）、點B（-1，0）和點C（1，0）分別是三條直線PQ，QR，RP上的點（A，B，C與P，Q，R均不重合），且直線PR，PQ是“P₁共軛線對”，直線QP，QR是“Q₄共軛線對”，直線RP，RQ是“R₉共軛線對”，求點P的坐標；
  （2）已知點

  Q

  （

  -

  1

  ，-

  2

  ）

  ，直線l₁，l₂是“Q_-2共軛線對”，當l₁的斜率變化時，求原點O到直線l₁，l₂的距離之積的取值范圍．
  組卷：92引用：3難度：0.5

  解析